page 12 

Further Studies

BF 1975

1.  The Warminster Mystery

Warminster, Wiltshire, is allegedly a region rich in leys, and it has been claimed that leys of order 12 and 13 are to be found passing through here.  Now orders 12 and 13 are numbers so far above the norm of ley orders that the case merits special attention. 

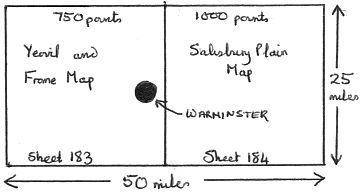
Fig. 11.

On the modern series of 1:50,000 OS maps, Warminster lies on the eastern edge of map 183 of the Yeovil and Frome region (already analysed in Case 8).  It transpired, however, that these high order leys fell not solely on this map, but ran over onto at least one neighbouring map – sheet 184 – of the Salisbury Plain, and so at least two maps were to be considered in conjunction.* Fig. 11 shows how these two maps fit together. 

* Case 8 introduces leys of this type. 

The two maps in conjunction contain of the order of 1750 ley points – sheet 183 containing about 750 (Case 8) and sheet 184 about 1000 (Case 2).  Of course, it is arguable that many of these are non-valid as ley points, so the calculations which follow will give results on the high side.  Bearing this in mind, we will retain n=1750. 

The combined area of the maps is A=2×625=1250 square miles. 

The mean length of a ley, L, since the maps taken together form rectangle 1 unit by 2 units, is 1.61×25 or about 40 miles. 

The ley width x is taken as 0.02 mile. 

Using the methods of Appendix 1, the expected alignments are:

N(4)	=	80990		N(9)	=	57
N(5)	=	30230		N(10)	=	8
N(6)	=	8465		N(11)	=	1
N(7)	=	1896		N(12)	=	0	.1
N(8)	=	354		N(13)	=	0	.01

These figures show the rich potentials of chance over this region, even accepting them as being on the high side.  Leys of order 8 or 9 can easily be the work of chance, and what are we to say of the evidential value of a ley of order 4 or 5? 

However, although the above figures to a large extent explain the richness of leys in this region, they do fall rather short of explaining the alleged high order leys consisting of 12 and 13 points respectively. 

A copy of The Ley Hunter (No. 45) gives a further clue.  In it Jimmy Goddard, one of the chief claimants for the Warminster case, traces one of the high order Warminster leys, and in addition to the usual classes of ley points, churches, tumuli, camps, moats etc. included in our 1750 points, he uses crossroads, hills, mileposts, and stretches of road.  Now on sheet 183 alone there are about 1800 crossroads, and goodness knows how many hills, mileposts or sharp bends in roads.  Even if half of these be discounted as modern, we still have here a dramatic increase in the number of ley points.  Assume then that in addition to the 1750 ley points we started out with, we have, on sheets 183 and 184 combined, a conservative further 1750 points belonging to Jimmy Goddard’s additional classes.  That means a total of 3500 ley points over the two maps combined.  Repeating our calculations with n=3500 we have:

N(4)	=	204800		N(11)	=	319
N(5)	=	152900		N(12)	=	71	.5
N(6)	=	85620		N(13)	=	14	.6
N(7)	=	38360		N(14)	=	2	.7
N(8)	=	14330		N(15)	=	0	.5
N(9)	=	4583		N(16)	=	0	.08
N(10)	=	1283

We now see that even in the case of this conservative estimate, the fact that Jimmy Goddard includes certain ley points which others would not, is sufficient to bring well within the bounds of probability those remarkable-sounding leys of order 12 and 13. 

 page 13 

2.  The UFO link

Certain ley line investigators, taking their cue from Aimé Michel’s theory of orthoteny, have come to the conclusion that ghosts and UFOs tend to be observed in the vicinity of ley lines.  Other investigators have tied in crimes of violence and motor-car accidents with ley lines also, and one group of investigators (The Ley Hunter, No. 50) have even observed a curious incidence of Post Offices falling on ley lines! 

The chance hypothesis here is that in certain regions there are sufficient ley lines about to make it quite likely that more or less any type of phenomenon will appear on or close to a ley line. 

As a preliminary experiment, I scattered 50 random points on a piece of graph paper, using random number tables to determine the points.  I then drew in all connecting lines of order 3 or more.  The picture obtained represented a square map and its 50 pseudo-ley points with the pseudo-ley lines linking them inserted.  A further 20 random points were then obtained in the same way, inserted on the map, and used to represent UFO sightings.  (See Graph 3.)

In three such experiments an average of just over 50% of the ‘sightings’ fell on the lines or close to the lines.  (This result was later verified by the methods of Appendix 2.)

This simple experiment, which the reader might like to repeat, is a useful pointer in that it shows that even with a low number of ‘ley points’ and thus a correspondingly low number of ‘ley lines’ dissecting the ‘map’, a surprising proportion of ‘sightings’ can be said to be ‘associated’ with the ley lines. 

Of course, the ley hunter’s map is larger than a sheet of graph paper, has more ley points on it, and the ley hunter usually counts alignments only when they are of order 4 or more.  Nevertheless, the above does constitute a primitive model. 

The next experiment – not to be recommended to those of little patience – was to scatter 50 random points (again using random number tables) onto a sheet of graph paper and to join each point to every other, continuing the line to the edges of the graph paper in each case.  About 1100 distinct lines are thus obtained, splicing the map into, in the vast majority of cases, minute little regions too small for a sighting to land in without automatically becoming associated with a line.  In many places the paper is black with pencil lines, and in only a few places does a large enough space occur to permit any chance of an ‘unattached’ sighting.  (See Graph 4.)

Now of course most of the 1100 lines are of order 2 or 3 and would not count as ley lines, But a map 25 miles square containing about 330 ley points would result in about 1100 genuine ley lines (i.e. of order 4 or more) when the adopted ley width was 0.02 mile, so that, if all the true ley lines were drawn in on such a map, the result would look rather like our piece of graph paper – with very little room for UFOs, accidents or Post Offices to avoid falling on a line. 

But the UFO ley hunter does not see things from this angle, or at least, if he does, either he has failed to insert all possible ley lines on his map (very easily done if he does not approach his task in a highly systematic manner) or his definition of a ley line begins at at least order 5, or possibly even more.  Another possibility, of course, is that he drafts his sightings onto the map and then looks to see if they fall on a ley line. 

Proceeding in this manner, I took an old 1-inch OS map, sheet 159, of the Chilterns, ringed all churches, earthworks, moats etc. (just over 560 points in all), and, using random number tables, drafted six ‘UFO sightings’ onto the map.  Each UFO sighting was represented by a small circle about 1/10 inch in diameter – corresponding to locating the UFO position from the sighting to within 200 yards – not an unreasonable limit of error.  (See end of Appendix 2 for drafting procedure.)

All six simulated UFOs were found to lie not simply on a single ley, but at the intersection of at least 3 leys of order 4 or more!  (See Fig. 12 for two examples.)

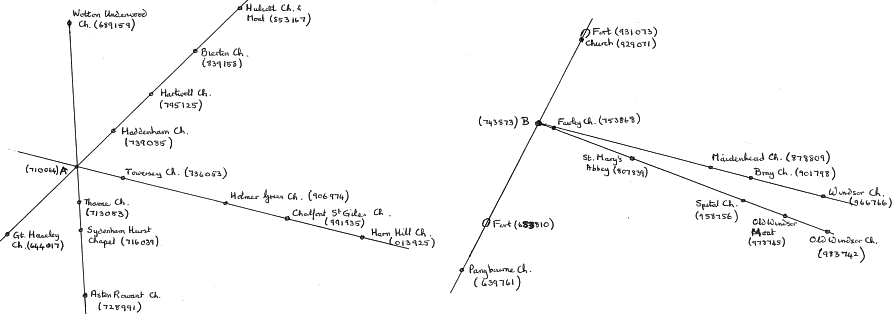
Fig. 12.  Two examples of ley lines passing through randomly simulated ‘UFO sightings’ on an old 1″ map of the Chilterns, sheet 159.
A and B are the ‘sightings’, being the first two of the six cases treated.

 page 14 

A chance hypothesis model for this map, using the methods of Appendix 2, predicts any UFO sighting to lie at the intersection of about 5 leys of order at least 4.  The results actually obtained using sheet 159, therefore, seem to be well in accord with the chance hypothesis. 

One of the chief proponents of the UFO link is Philip Grant, who has written several articles on the topic.  He has worked using six 1-inch OS maps in conjunction, covering about 4000 square miles and, at a conservative estimate, 3000 potential ley points (500 per map) – see Fig. 13. 

Fig. 13.

Calculation shows that such a composite map, containing 3000 points to be aligned to within x=0.02 mile, will contain about 352,000 leys of order at least 4, amongst which will be about 18 leys of order ten.  The following table gives the complete and almost unbelievable list of expected alignments:

N(4)	=	238000		N(9)	=	134
N(5)	=	85040		N(10)	=	17	.9
N(6)	=	22800		N(11)	=	2	.1
N(7)	=	4886		N(12)	=	0	.2
N(8)	=	873

Calculation also shows that any UFO sighting (or murder, car accident, or even Post Office) on this composite map will be at the junction of, on average, 136 leys of order at least 4! 

Philip Grant claims (The Ley Hunter, No. 50) that 90% of ghosts and UFOs in this region occur on leys; that all the local ‘puma’ sightings occur on leys; that “schools, cemeteries and public buildings of all kinds (including, crazy though it may sound, post offices) fall on leys too often for pure coincidence”; and that various local landmarks, water towers and contemporary buildings fall on leys also. 

I, for one, am not surprised. 

 page 15 

3.  The Triangular Puzzle

Case A.In his popular book The Dragon and the Disc, F.W. Holiday claims to have rediscovered an intricate system of right angled triangles stretching from Pembroke to Wiltshire.  The hypotenuses of these triangles are alleged to point towards various azimuthal values in the North West (not specified), and Holiday believes that “much of Britain was thus covered” (p. 144). 

How is chance to explain this?  I have not done extensive research into Holiday’s system, but the following remarks may serve as a pointer. 

If the reader was surprised by the number of distinct alignments to be expected amongst n random points, he will be even more so by the number of possible triangles which can be defined by those points. 

For example, 200 points will define some 14,600 distinct lines (on a map 25 miles square, with, x=0.02 mile) and yet some 1.3 million triangles!  To coin a phrase, that is an awful lot of tickets to own in a lottery, even your chances of winning are very slight indeed. 

These 1.3 million triangles, of course, are all shapes and sizes, and we are interested in those particular ones which are right angled. 

How many right angled triangles could we expect to find with their vertices defined by ley points? 

It can be shown (see Appendix 4A) that amongst n random points, the number of such will be, on average, given by:

N(Rt.)= n(n−1)(n−2) p 2

where  p=xL/A  as defined in the Introduction. 

With 200 points, therefore, on a map 25 miles square and with x=0.02 mile, we can expect:

N(Rt.)= 200×199×198×0.000864 =3404 2

right angled triangles, having of course various shapes, sizes and orientations.  That is quite a large number from which to select those whose hypotenuses point ‘to various azimuthal values in the North West’ – or any other direction for that matter.  (Even with only 50 ley points to play with, there will be about 51 right angled triangles defined!)

For this reason I would suspect that it is chance which is at the root of Holiday’s Figs. 14 and 15, and not “the incredible surveying task undertaken in Britain some 2000 years B.C. for purposes yet unknown” (p. 144). 

Case B.Another triangular puzzle is to be found in Sir Norman Lockyer’s Stonehenge and Other British Stone Monments, Ch. XL, the contention here being that Stonehenge, Grovelly Castle and Old Sarum define the vertices of an equilateral triangle of side close on 6 miles. 

It must be said at the outset that this case is more of a puzzle than Case A.  However, let us see what sort of things chance can produce. 

How many equilateral triangles can we expect to find defined amongst n random points?  If ε is the admissible error in the sides, then amongst n points it can be shown that we can expect:

N(Eq.)= 8n(n−1)(n−2)ε2 3√3A

equilateral triangles (see Appendix 4B). 

Now there are two principal facts about the Stonehenge Triangle:

• (a) its vertices are defined by prominent sites. 
• (b) the sides of the triangle are all close to a whole number of miles (i.e. 6 miles) with error ±0.1 mile, the sides being taken as the centre to centre distances. 

On the 1:50,000 OS sheet 184 of Salisbury Plain there are about 1000 ley point contenders (see Case 2), so that if any site were admissible as a vertex, there would clearly be a large number of equilateral triangles to be found. 

In accordance with clause (a), therefore, I counted only prominent sites – large earthworks and camps etc.  I counted about 50, but as the definition of ‘prominent site’ is rather vague, there is some room for doubt here.  The figure may be higher or lower.  Nevertheless, let us take 50 as an estimate. 

 page 16 

With n=50, A=625 square miles and ε=0.1 mile, the formula gives:

N(Eq.)= 8×50×49×48×0.12 =2.9 3√3×625

and this is the number of ‘prominent site’ equilateral triangles to be expected of the accuracy of the Stonehenge case presented by Lockyer. 

Which leaves us with the fact that the sides of Lockyer’s triangle were all close to an integral number of miles in length. 

The probability that a measured distance will be within ±0.1 mile of an integral number of miles is about 0.2. 

The expected number of equilateral triangles having this property, therefore, is about 0.2×2.9=0.58 – i.e. on maps like the 1:50,000 OS sheet 184, containing the same number of prominent sites etc., we should expect to find such a case as that presented by Lockyer on just over half the maps investigated. 

But then there are other considerations in this case: the line joining the centres of Grovely Castle and Stonehenge points towards sunrise on the longest day, for instance.  This is certainly true, though the claim that the oldest crossroads on Salisbury Plain lies at the centre of the triangle (it is about 0.2 mile from the circumcentre) is rather more suspect. 

All that can be said is that from our first assumptions (prominent sites; integral lengths) the triangle could be a chance effect but that the issue must remain unsettled in view of at least one further consideration.  Certainly a case of some interest. 

 page 17 

4.  Major Tyler’s Geometrical Arrangements

(Relevant to The Geometrical Arrangement of Ancient Sites, by Major F.C. Tyler, O.B.E., Simpkin Marshall Ltd., 1939.)

Major Tyler’s geometrical theorisings present a deceptively impressive set of geometrical ‘arrangements’ besides the usual ley line networks, one of which was studied in Case 10. 

The first which we consider here concerns Stonehenge and an array of twenty-three concentric circles centred, curiously enough, not on the centre point of Stonehenge itself, “but on a point on the western side of the enclosing vallum” (p. 35.) (Why the centre of the system should be here remains, like the reason for leys tending to skirt large points rather than pass through their centres, a mystery.)

Furthermore, each of these twenty-three circles has a radius which is a multiple of the alpha unit (950.4 feet or 0.18 mile) and each circle or arc passes through a minimum of two ley points.  The highest order circle passes through 8 points.  To quote Major Tyler:

“The sites which are taken up by the circles shown in the diagram include – besides the larger earthworks – small tumuli and churches.  One circle has on it as many as eight sites, of which as many as six are quite small tumuli.  Other circles take up: some, three sites; three circles, four sites; two circles, five sites; two circles, six sites; and the one circle mentioned, eight sites.”

The minimum requirement for the insertion of a circle, however, is that two points lie on it. 

The important point is that these twenty-three circles, though all multiples of 950.4 feet in radius, are merely a selection from the set of circles with this particular centre and this particular radius property.  Imagine a square map, Stonehenge at its centre, covering an area 25 miles by 25 miles, then there are 12½/0.18=69 such complete circles.  (Circles of radius larger than 12½ miles, which fall partially off the map, are ignored for the present – see Fig. 14.)

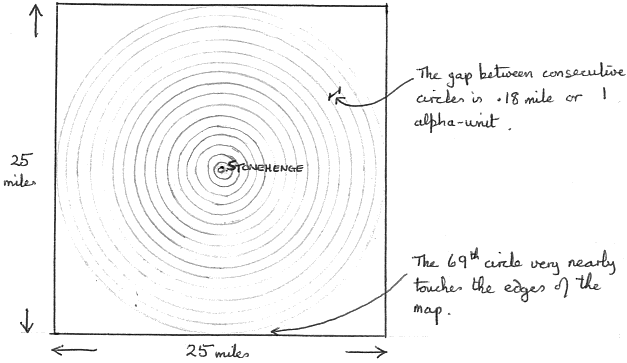
Fig. 14.  Major Tyler’s Stonehenge case.

This is the first clue.  If the alpha unit circles are so important, why use an apparently haphazard selection of 23 from 69 on which to place two or more monuments? 

The chance hypothesis model is therefore as follows: sprinkle ‘points’ randomly over the map and calculate (a) the expected number of circles out of the 69 possible which will pass through at least two points; (b) the probability that a circle (any circle of the system – Major Tyler mentions no specific multiple of the alpha unit here) will contain at least 8 points. 

As with ley lines we now face two problems. 

Firstly, how many points are we to ‘sprinkle’ on the map?  An investigation of this region (see Case 2) revealed about 1000 ley point contenders, and so we will assume this figure.  How many are non-valid as ley points out of the 1000 remains to be seen, but for the present we are merely investigating the potential of chance, so we will let the figure of 1000 stand and bear in mind the possibility that this is high. 

Secondly, like ley lines, the circles have ‘width’.  They are not so much circles as thin annuli.  How thin?  Well, since they involve ley points, about as thin as ley lines – i.e. about 0.02 mile. 

Analysis reveals (see Appendix 3A) that scattering 1000 points on a map 25 miles square, containing concentric annuli (centred on the mid point of the map) whose radii are multiples of the alpha unit, and whose widths are 0.02 mile, would result in:

(a) about 24 ‘circles’ containing 2 or more ‘points’.*

* With 750 points, all else staying the same, 17 circles would be obtained. 

(b) a probability of about 0.04 or 1/25 that at least one ‘circle’ would pass through at least 8 points. 

 page 18 

In Tyler’s Fig. 9, the eleventh circle from the centre is the one of order 8, and we are told that of the eight points, six are quite small tumuli.  What the other two are, we are not told directly, but from his Fig. 9 it is possible to hazard a reasonable guess. 

It would seem fairly probable that one of the points is Charlton Church (1:50,000 sheet 173; 118560) and that the other is Todford Circle (1:50,000 sheet 184; 983405).  If this is so, then since the second ‘point’ is a large point (mean width on map 4.5 mm, ocorresponding to about 0.14 mile), the alleged circle of order 8 is properly only one of order 7.  The chance hypothesis predicts at least one circle of at least this order with probability 0.15. 

In conclusion therefore, Major Tyler’s Stonehenge case is within the bounds of chance on two counts: (a) the total number of circles or arcs involved in the system, (b) the reasonable likelihood of some fairly high order circle occurring somewhere in the system. 

Elsewhere in Major Tyler’s little book, we find two other concentric-circle systems – one centred at Wooburn, Bucks., and the other at Churchingford, Devon.  It is significant that in neither case does Tyler make any stipulation about the radii of the circles involved being multiples of the alpha unit.  Let us look at the Wooburn case – Tyler’s Fig. 3. 

Taking a 25 mile by 25 mile square, its centre at Wooburn, in which the system roughly falls, analysis reveals:

Churches	614
Tumuli, Camps etc.	23
Moats	30
Miscellaneous	14
	681

(Data compiled from 1-inch OS maps 159 and 160.)

Let us assume 400 valid ley points. 

If the circles had to have radii which were multiples of the alpha unit, the chance hypothesis (by the methods of Appendix 3A) predicts a system of 7 concentric circles, each passing through at least two points. 

If the alpha unit stipulation be dropped, then the field is opened considerably, and calculation shows (by the methods of Appendix 3B) that from our 400 points we can expect 66 concentric circles, once again, each circle passing through at least two points.  If only 200 points were valid, we could expect 21 circles under the same criteria. 

Major Tyler’s Wooburn system consists of 25 circles, thus falling well within the bounds of chance. 

Further, the system also includes a series of 8 ley lines, each of order at least 4, radiating from Wooburn church at the centre of the system.  The methods of Appendix 2, for 400 points, predict 14 such lines, so Major Tyler’s Wooburn system falls within the bounds of chance on this count also. 

To show the power of chance in operation in a practical test, a simulation of the Wooburn case was constructed.  150 random points were drafted onto a sheet of graph paper, one point being placed at the centre of the sheet to represent Wooburn church.  Circular arcs centred on the pseudo-Wooburn were then inserted whenever such arcs passed through at least two ley points.  Leys of order three or more passing through the centre were then inserted after the manner of Major Tyler’s Fig. 3.  (See Graph 5.)

Obtained were: 24 circles or arcs, and 31 leys through the centre point (25 of order 3 and 6 of order 4). 

Predicted were: 26 circles or arcs, and 34 leys through the centre point (28 of order 3, 5 of order 4, 1 of order 5 or more).