Update to Appendix 4B: Equilateral Triangles of Sites

Michael Behrend, 2014

Here we assume n points have independent uniform distributions in a region K (typically a disk or square), and estimate the expected number of near-equilateral triangles formed among the points. There are several reasonable definitions of “near-equilateral”. Bob Forrest’s definition here is: A triangle PQR is near-equilateral iff there is a side (say PQ) such that the other two sides (PR, QR) differ from PQ in length by less than some predefined small value ε.

To avoid difficulties with a near-equilateral triangle being picked up more than once, note that if the above condition holds for some side PQ then it must hold for the side of middle length. Accordingly, we find the probability p that PQR is near equilateral assuming that

PR<PQ<QR
P, Q, R run anticlockwise round the triangle.

The expected number of near-equilateral triangles is then ⁿC₃×12×p, where the factor 12 arises from ×6 for the order of the lengths PQ, QR, RP, and ×2 for the orientation.

Lozenge-shaped area in which point R must fall

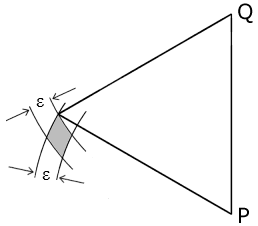
For a given P and Q, the vertex R is required to fall inside the small lozenge shown in the diagram. (This is similar to Bob Forrest’s diagram, but the lozenge is only half the size of his in each direction.) The sides of the lozenge are circular arcs, but since ε is small we assume they are straight lines, so that area of the lozenge is 2ε²/√3.

It is also necessary for this lozenge to fall inside K. We thus need to answer the question: if points P and Q have independent uniform distributions in a region K, and R is the point such that PQR is an anticlockwise equilateral triangle, what is the probability τ that R falls inside K? One way to tackle this is: Let P be a point in K, rotate K through 60° about P to a new position K′, and let φ(P) = area(K ∩ K′)/area(K). Then τ is the mean value of φ(P) when P is uniformly distributed inside K. This leads fairly easily to

τ(circle)=1−3√3/4π≈0.5865

and with more difficulty to

τ(square)=15/2−4√3≈0.5718.

Putting the above together, and denoting by A the area of K, we find that the expected number of near-equilateral triangles among n points with independent uniform distributions in K is

(4τε²/√3A) n(n−1)(n−2).

This formula was checked against 100,000 simulations for Lockyer’s triangle in Further Studies: 50 points in a square of side 25 miles, with tolerance ε=0.1 mile. The expectation calculated from the formula is 3.2449 near-equilateral triangles, and the mean of the simulations was 3.2457.

Bob Forrest’s estimate was 2.9, so his conclusions are not materially affected by this update.