page 22

Appendix 2: Vertex Analysis

BF 1975; “two versions” MB 2014

The question here is one of ley-centres – i.e. ley points which lie at the intersection of several ley lines. For the chance hypothesis, we select some ley point O and join it up to all the other ley points on the map. We seek the average number of leys of various orders that we can expect to find passing through O.

Let there be n ley points on the map.

The will be a maximum of n−1 lines passing through O. In practice, there will be less than this since, to within the alignment limit x, some will coalesce; e.g. in the figure, OP₄ and OP₅ merge to give a ley of order 3, and OP₂, OP₈, OP₉ merge to give a ley of order 4.

A ley point O joined to ten other ley points

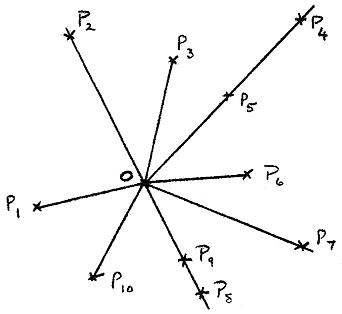
Let there be K distinct leys through O, including simple order-2 leys (e.g. OP₃), and let N′(r) be the number of leys of order r passing through O. If P(r) is as in Appendix 1, then we have:

N′(r)=KN(r)

(1)

K=N′(2)+N′(3)+⋯+N′(n)

(2)

n−1=N′(2)+2N′(3)+⋯+(n−1)N′(n)

(3)

By (1) and (3),

n−1	=K [P(2)+2P(3)+⋯+(n−1)P(n)]

n−1	=K	∑	^j⁼ⁿ	( j−1)P( j)
			_j₌₂

whence

K=(n−1)	/	∑	^j⁼ⁿ	( j−1)P( j).
			_j₌₂

(4)

It can be shown, by differentiation of the generating function of P( j )=e^−np(np) ^j⁻²/( j−2)! for j=2,…,n, that the denominator of (4) is given by

∑	^j⁼ⁿ	( j−1)P( j)=1+np
	_j₌₂

and so (4) simplifies to

K=	n−1
	1+np

(5)

Once K is known by (5), N′(r) can be found using (1), and hence we are able to determine the average number of leys of order 2, 3, 4, 5, etc. to be expected to pass through any ley point O.

2014: For further discussion, see the update to Appendix 2

Applications

1. To Major Tyler’s Wooburn case

A total of 637 ley point contenders was counted over the region covered by Tyler’s Fig. 3.

If we assume 400 of these are valid, then with n=400, x=0.02 mile, L=27 miles, A=625 sq. miles, we have K=297 by (5), from which

N′(3)	=	72	.6
N′(4)	=	12	.6
N′(5)	=	1	.4
N′(6)	=	0	.1

page 23

Major Tyler presents us with five 4-point leys and three 5-point leys passing through Wooburn Church. One of the 5-point leys is shown to ‘skirt’ an earthwork (point 55), and is thus possibly strictly only a 4-point ley, making Tyler’s result: six 4-point leys, two 5-point leys.

Further, if 500 of the ley-point contenders are valid, then, still with x=0.02 mile, L=27 miles, A=625 sq. miles, we have

N′(4)	=	21
N′(5)	=	3
N′(6)	=	0	.3

Major Tyler’s leys through Wooburn, therefore, do not appear to transcend chance.

2014: This conclusion has been confirmed by computer simulations

2. Tyler simulation

This simulation is described at the end of Further Studies.

With n=150, x=0.025 mile, L=11×1.08=11.9 miles, A=11²=121 sq. miles, we have K=109 and alignments through the centre of order 3 or more number 33.6. In the actual simulations, 31 were obtained.

2014: See update for results of computer simulations

3. The UFO link

Draft a UFO sighting onto the map, and consider it exactly as if it were a ley point. If n is large, then joining up the UFO to all the surrounding ley points will result in about the same number of ley lines as if a ley point itself had been joined to it, but with one difference. N′(r) is now the number of ley lines of order r−1 passing through the UFO (see figure).

Figure B: UFO sighting versus ley point as a centre

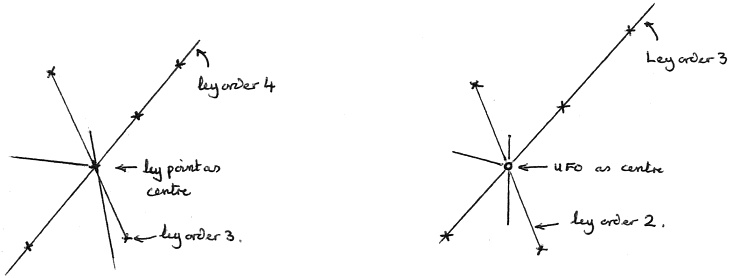
Thus application of our methods to the case of UFO sighting as centre gives:

N′(2)=	no. of lines containing only	1	point, passing through UFO sighting
N′(3)=	„	2	„
N′(4)=	„	3	„

etc.

page 24

On the 1-inch OS sheet 159 considered in Further Studies just over 560 sites were ringed. Take n=560, x=0.02 mile, L=27 miles, A=625 sq. miles; then K=377 and

N′(3)=	112		order	2	leys through UFO
N′(4)=	27		„	3	„
N′(5)=	4	.4	„	4	„
N′(6)=	0	.5	„	5	„

The figures for the Philip Grant case in Further Studies are with n=3000, x=0.02 mile, L=1.34×50=67 miles, A=6×625=3750 sq. miles, leading to K=1448 and thus, on average, 136 leys of order at least 4 pass through any UFO sighting.

Procedure for simulations of UFO sightings

A string of 36 random numbers (the first row of Table 8 in the Cambridge Elementary Statistical Tables) was taken:

2017 4228 2317 5966 3861 0210 8610 5155 9252

and grouped in pairs of threes as follows:

(201, 742), (282, 317), (596, 638), (610, 210), (861, 051), (559, 252)

These are then used to determine grid references as follows:

x	y	X=x×40	Y=y×45	X+63	Y+73	UFO grid ref.
0.201	0.742	8.04	33.39	71.0	06.4	710	064
0.282	0.317	11.28	14.27	74.3	87.3	743	873
0.596	0.638	23.84	28.71	86.8	01.7	868	017
0.610	0.210	24.40	9.45	87.4	82.5	874	825
0.861	0.051	34.44	2.30	97.4	75.3	974	753
0.559	0.252	22.36	11.34	85.4	84.3	854	843

The map is 40 grid squares by 45 grid squares. Hence x×40 and y×45.
The map origin, or lower left-hand corner, is 630 730. Hence X+63, Y+73.
The columns X+63, Y+73 are modulo 100 and correct to 1 d.p.

A similar type of procedure is adopted in the other UFO-link simulations (both UFOs and ley points) as well as for the ley points in the East Anglia simulation and Major Tyler’s Wooburn simulation.