The Ulro Papers: No. 1.
Why I do not believe the Great Pyramid to be a very mystical edifice
being a compilation of some preliminary results towards the
demystification of the said edifice
by
Robert Forrest
Long Time Professor of Doubt at
the University of Leyland.
Author of: Number Mysticism and
Winnie the Pooh; Introduction to
Sci-Phi; etc etc.
To All Mad and Merry Mystics This Paper is
aimed and dedicated by the
author.
“You were best to go to bed and dream again.” (2 Hen VI. v. 1.)
“And that, knowing the time, that now it is high time to awake out
of sleep: for now is our salvation nearer than when we believed.” (Romans 13:11.)
MCMLXXVII
*******
1. The pi theory
The Egyptian equivalent of our pi was 3.1605, NOT 3.1416. The Egyptians simply
did not know our value of pi, so they could hardly have featured it intentionally
in the Great Pyramid.
2. Connolly’s “Rolling Drum”
(see K. Mendelssohn, “The Riddle of the Pyramids” p. 73.)
Connolly's rolling drum idea was an ingenious explanation of why our pi should
appear in the G.P. and not the Egyptian pi. It also gives a good explanation of the
change in angle of slope of the Bent Pyramid. But on the other hand, it doesn’t
fit other pyramids (e.g. Chephren) very well.
The conservatism of the Egyptians and the practical nature of their mathematics
suggest that the techniques of pyramid design and construction were standard. It
would seem desirable that any theory of pyramid design should apply also to other pyramids.
3. The phi theory
Again, although the phi theory holds well for the G.P. it doesn’t appear to
hold for other pyramids.
Also Egyptian maths was very cumbersome, so that the Egyptians would not
have been able to calculate phi at all accurately. If they had known the theorem of
Pythagoras, and had they known even the rudiments of theoretical geometry (as
opposed to practical) then they might have been able to accurately construct phi.
But (R.J. Gillings “Mathematics in the Time of the Pharaohs” Appendix 5)
there is no evidence that the Egyptians knew the Pythagoras theorem. In fact it appears
that Egyptian Geometry never actually reached the heights later attributed to it
by the Greeks.
So like the pi theory before it, the phi theory is inconsistent with what is known
of Egyptian mathematics, and it would appear likely that both pi and phi are unintended
side-effects superimposed on an innocent pyramid by essentially modern imaginations.
(Note: the pi theory implies the phi theory as a side-effect, and vice versa, so
we are not claiming here a double accident – merely an interesting single one. This
follows from the known coincidence of numbers that
4/π ≈ √φ.)
4. The Equation of Herodotus
It is frequently stated that the area of a square on the height of the G.P. equals the
area of a G.P. face. This is known as the Equation of Herodotus, because it is commonly
believed that Herodotus said this (Tompkins “Secret of the G.P.” p. 190.).
In fact, Herodotus didn’t say this – it was John Taylor who ‘interpreted’
what he said in this way, and it is this interpretation
which has been repeatedly quoted as the Equation of Herodotus.
The commonest translation of Herodotus II:124 reads: “It is a square eight hundred feet
each way, and the height is the same …”.
How and Wells in their “Commentary on Herodotus” (1912), vol. 1, p. 228,
claim that height in this passage refers to slant height. This agrees with a conclusion
reached independently by myself: Herodotus believed that the G.P. faces were equilateral triangles.
The Equation of Taylor (as opposed to Herodotus) would, intentionally or
otherwise, have given rise to the pi and phi properties attributed to the G.P. But
as I say, this is the Equation of Taylor, and not, as is so commonly claimed, the
Equation of Herodotus.
5. Pythagoras
Gillings (above) reports that there is no evidence at all that the Egyptians
were familiar with the Pythagorean Triangle – not even the simplest 3:4:5.
There is a reference in Plutarch’s “Of Isis & Osiris”, but this is open to a
charge of Greek ‘intrusion’ into Egpytian maths.
Two commonly alleged uses of the 3:4:5 are: a) in the slope of Chephren’s
Pyramid at Giza (this was believed by Petrie: Pyramids & Temples of Gizeh. 1883)
and b) in the King’s Chamber of the G.P.
(Tompkins p. 101; Ivimy p. 125–6.)
b), in accordance with the principle of “in our attempts to decide how the
Egyptians decided upon the design & proportion of the G.P., we should take care
not to go beyond the known limits of Egyptian mathematics”, I would tentatively
reject, in view of Gillings. In fig 1 I give a very much simpler explanation of
the Kings Chamber design based solely on the use of the double-square.
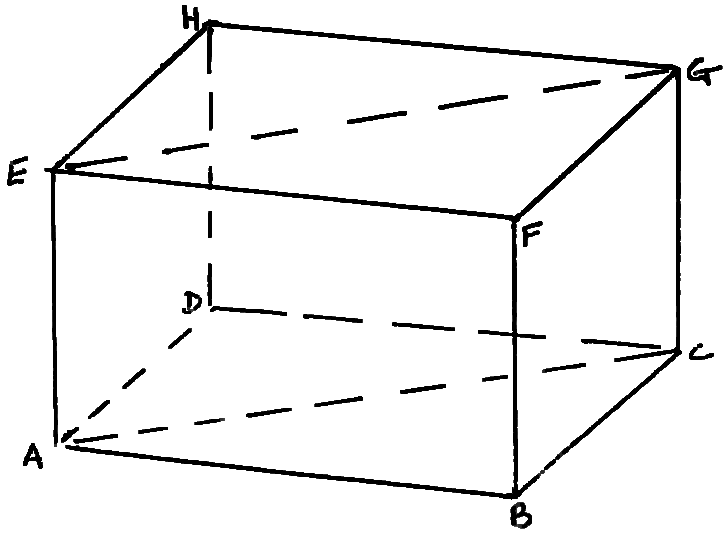
Fig. 1. Proposed Construction of Kings Chamber.
The floor was laid out in the form of a double square. The height of the chamber was then taken to be half the floor diagonal, thus making the diagonal cross-section of the chamber a double square also.
In the diagram, ABCD is a double square.
If the Egyptians had intended to make ACGE also a double square, they would also, without knowing it, have made triangle ABG a 3:4:5 triangle.
Part a) I will deal with below.
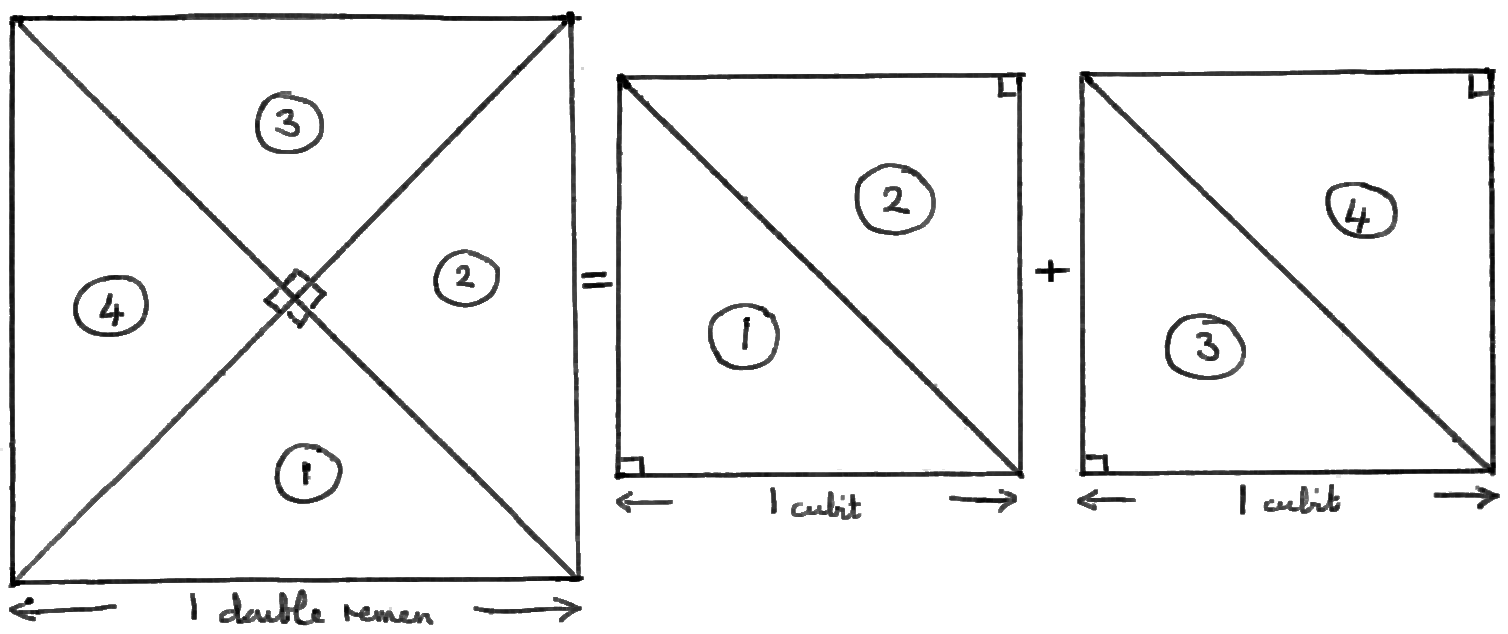
The definition of the double remen (= √2 cubits) seems to suggest Pythagoras
(cf. extension of this idea in "City of Revelation" p. 106), but here again this is a modern
interpretation of a practical result. The double remen appears to have come into use for
“doubling up” areas of land. A field of side x by y double
remens has exactly double the area of a field x by y cubits.
“Doubling up” was very much a feature of cumbersome Egyptian arithmetic,
and the derivation of a double remen by a practical exercise involving areas, and with
no concept of Pythagoras at all, is featured in fig. 2.
Fig. 2. The area of the 1 double-remen square is double the area of a 1 cubit square.
6. Practicalities
(In this section RMP56 means problem study 56 in the Rhind Mathematical Papyrus.
See Gillings for details.)
In accordance with the criteria of simplicity & consistency with known Egyptian
Mathematics, the following present themselves:
- the Egyptian units of measurement: 1 cubit = 7 palms; 1 palm = 4 fingers.
-
in measuring pyramid slopes the Egyptians used
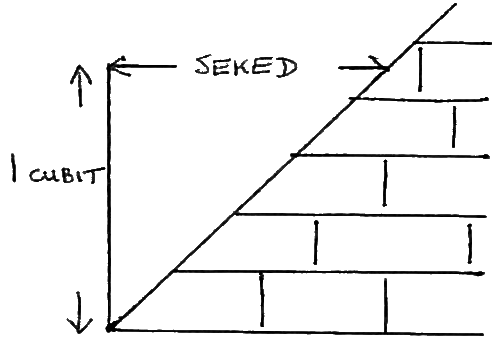
“seked” = horizontal displacement per 1 cubit rise (see fig 3)
Fig. 3. Definition of the seked
RMP 56–60 inclusive concern pyramids and their sekeds. In particular RMP 57–59 incl.
concern pyramids with sekeds 5 palms 1 finger, or, as we would measure it, a slope of
arc cot 5¼/7 =
arc cot 3/4, which is of course
the slope of Chephren’s Pyramid but without recourse to the 3:4:5 triangle,
though of course giving the same ‘end product’ as the use of that triangle.
The Great Pyramid, on the other hand, is accurately described by a seked of
5 palms 2 fingers, or, as we would say, a slope of
arc cot 5½/7 =
arc cot 11/14, and from this it easy to see
how the pi illusion (and hence the phi delusion) came to arise.
And Mycerinus? Petrie gives 51° 0′ ± 10′ as its slope.
A seked of 5 palms 3 fingers would imply an angle of slope of 50° 36′.
And the bent pyramid? The lower portion conforms to a seked of 5 palms, and the
upper to a seked of 7 palms 2 fingers (though the latter is 0.3 degrees out, so not
satisfactory; the actual slope falls between a seked of
7½ palms & 7¼ palms.)
In conclusion, therefore, using only a practical approach involving sekeds of
palms and fingers, and using no mysticism whatsover, the Giza Group as a whole,
plus at least half of the Bent Pyramid (!?!) follow the same angle-of-slope design
principle.
To finish with a passing fancy: the Great Pyramid, with its seked of 5 palms
2 fingers: in view of the volume of bizarre literature centred about the Great Pyramid,
those 2 fingers (like the
indication of Merton Sewage Works
– FT 18, p. 15),
carry a wickedly symbolic messsge for posterity …
Robert Forrest. March 77.
Quotation from Encyclopedia Britannica
“The Egyptians were a practical people, and they reveal through the products of
their arts and crafts their particular genius. In classical times these early
Egyptians were also credited by the Greeks with great knowledge and wisdom; but the
evidence provided by Egyptian writings does not support this Greek opinion. It is
probable that Greek travellers in Egypt, impressed by the grandeur and antiquity of
the monuments of the land and misled by the accounts of past ages given to them by
their priestly guides, grossly misinterpreted the evidence and jumped to unwarranted
conclusions. Unlike the Greeks, the Egyptians were not philosophically inclined,
intellectually inquisitive, or prone to theorising. They tended to accept the world
as they saw it and to make use of its advantages without looking too deeply into the
properties of its parts. They were good engineers and builders, but not good
mathematicians, limiting their interest in calculation to the solution of practical
problems.”