Back in the nineteenth century, it was discovered that all knowledge in the universe is locked up in the Great Pyramid. Since then, there have been countless attempts to unlock this vast store of information, but success has been limited. As Bertrand Russell noted, the pyramid is excellent at explaining the past, but never quite manages to predict the future. [1]
Of the various numerological questions posed by the pyramid, the most interesting is the question of its slope. There were two primary schools of thought in the nineteenth century. One held that the pyramid “squares the circle,” that its perimeter divided by its height is exactly 2π. The other held that the pyramid was built to the proportions defined by the Golden Ratio, because long ago, the Egyptians told Herodotus that the pyramid was built so that the area of each face is equal to the area of a square whose side is the height. [2]

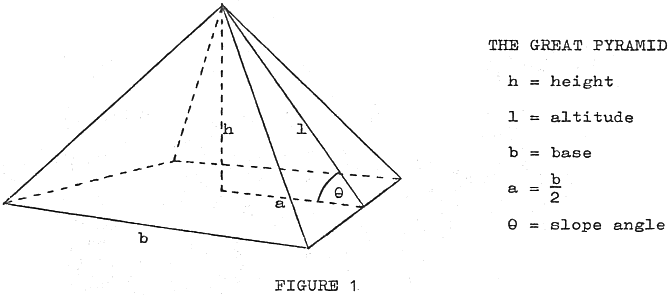
Referring to Fig. 1, the circle-squaring theory holds that 4b/h = 2π. This implies that the slope angle θ = 51° 51′ 14″.
The Golden Ratio argument is more subtle. The Ratio is φ = (1 + √5)/2, or 1.61803398+. According to Herodotus, h2 = bl/2 = al. Also, from the Pythagorean Theorem, l2 = a2 + h2. Then, substituting, l2 − al − a2 = 0, or, if x = l/a, then x2 − x − 1 = 0. The solutions are x = (1 ± √5)/2 so the positive solution is φ, and secθ = φ. Furthermore, h/a = √φ, so tan2θ = φ also. These equations imply that θ = 51° 49′ 38″.
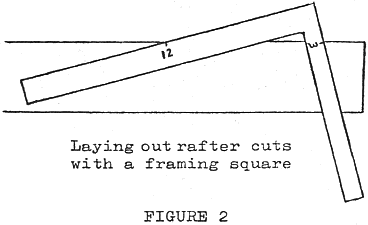
A carpenter doesn’t use a protractor to lay out most angles. He uses his framing square. So, roof pitches are not measured in degrees, but in inches of rise per foot of run. Modern low roofed houses commonly have about a “three-twelve” pitch, which is approximately 14°. Fig. 2 shows how a carpenter lays out his rafter cuts for such a pitch.
According to Willy Ley [3], the Rhind Papyrus shows that the Egyptians handled angles in a similar fashion, but used cotangent rather than tangent. Also, the basic unit used in pyramid building was the royal ell, which, equalled seven palms. One of the problems in the Rhind Papyrus (a sort of math workbook) requires the student to figure dimensions of a pyramid with a slope of 5½ palms per ell. That is, cotθ = 5½/7, or θ = 51° 50′ 34″.
A glance at the table in Fig. 3 shows that the values of θ implied by the three theories are remarkably close. In fact, if the original base of the pyramid was 765 feet, the difference between the height. implied by the Golden Ratio (the minimum) and the height implied by Pi (the maximum) is just over 5½ inches. As the casing and capstones of the pyramid have been missing for centuries, its original height can only be estimated within a couple feet.
| Basis | Angle | Height |
|---|---|---|
| square circle | 51° 51′ 14″ | 487 ft. 0.17 in. |
| Golden Ratio | 51° 49′ 38″ | 486 ft. 6.57 in. |
| 5½ palm pitch | 51° 50′ 34″ | 486 ft. 9.82 in. |
Egyptian mathematicians were crippled by an abominable system of arithmetic. There were signs for 1, 10, 100, etc., up to 1,000,000, but they had no efficient way of writing 2, 30, 400, etc., which were formed by repetition. So, to write 999, one had to make twenty-seven signs. They didn’t carry the multiplication table above two, so to multiply by seven, they doubled a number once, then again, then added double the number and finally added the original number. [4] I just worked the problem 937 × 876 = 820,812 in twenty-five seconds. An Egyptian mathematician might have struggled with it for half an hour.
Fractions were also a trial. With the single exception of 2/3, all fractions were reduced to the sum of fractions having numerator one. They had tables for doubling fractions, so that 2 × 1/19 = 1/12 + 1/76 + 1/114, but even with the aid of tables, multiplying one fraction by another must have been a nightmare. [5]
Because of the limitations of their numerical system, the ancient Egyptians never determined a good numerical value for Pi. For computing areas, they assumed that the area of a circle is equal to the area of a square with sides eight-ninths the diameter. From this, π = 4(8/9)2 = 3.1604938+, an error of about 0.6%. Ignorance of the true value of Pi didn’t hamper their building. If it was necessary to multiply by Pi, the distance was laid out by rolling a carefully made wheel the required number of revolutions.
So, the argument that the pyramid demonstrates Pi falls to Occam’s Razor. There is no direct evidence that the Egyptians had a decent estimate of the numerical value of Pi. On the contrary, their cumbersome system of arithmetic makes it highly unlikely that they did. While they might have laid out the pyramid with a wheel, there are better hypotheses available to explain the slope angle.
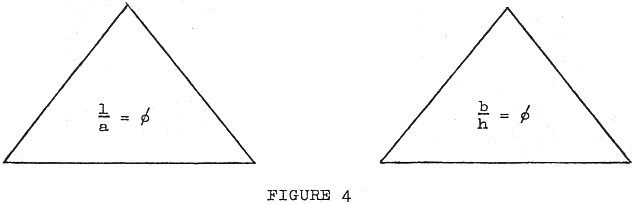
The Golden Ratio argument likewise collapses. The ancient Egyptians may well have built the Great Pyramid so that the area of a face equals the area of a square with sides equal to the height, as their descendants told Herodotus. Such a construction was well within their mathematical abilities. They also could have laid out the Golden Ratio, if they were interested. (They almost certainly didn’t know its numerical value, as computing √5 would have severely taxed their mathematical competence.) But why would anyone pick such a Mickey Mouse way of demonstrating the Golden Ratio? The ratio of the altitude of a face to half the base rhymes, but hardly grabs the eye. The square of the tangent of the slope angle is even more esoteric. If the Egyptians were hung up on the Golden Ratio, they could simply have built the pyramid so that b/h = φ. Fig. 4 shows two pyramids, one drawn so that l/a = φ, and the other so that b/h = φ. Can you see any difference? It would have shortened the pyramid by 13 ft. 9 in., and would have allowed them to use their favorite fraction for computing the pitch. A slope of 5 palms per ell gives the Golden Ratio within 0.06%, or 3 in. on the height of the pyramid. This would be absolutely undetectable to the eye, which the Golden Ratio is supposed to please.
I’m with Willy Ley. To me, the best hypothesis is that the Great Pyramid was built with a slope of 5½ palms per ell. It’s a simple, practical way of doing things, and we know that the Egyptians did figure angles that way. They could easily have computed that this pitch made the area of a face nearly equal to the area of a square whose sides equal the height, and they might have been pleased by the numerology of it. It’s also possible that they knew about Pi and the Golden Ratio, but, without evidence that they did, arguing about it is as profitable as arguing about the number of angels that can dance on the head of a pin.
Besides, I think there is compelling evidence that the Egyptians built the pyramid to a pitch of 5½ palms run per ell of rise. The key is another pyramid mystery, the empty “sarcophagus.” There’s no evidence that this hollowed rectangular block of stone ever held a mummy. It’s called a sarcophagus because it’s in an alleged tomb. But was it a tomb? Actually, the “sarcophagus” is quite similar to a modern crap table. The pyramid is hardly more pretentious than some casinos. And the ratio of the height of the pyramid to its base is seven-eleven! Could this be merely coincidence, Erik?
The End
| 1. | As quoted by Martin Gardner, Fads and Fallacies in the Name of Science, Dover Publications, 1957, p. 180f. |
| 2. | Gardner, op. cit., p. 178. |
| 3. | Willy Ley, Another Look at Atlantis and Fifteen Other Essays, Bell Publishing Co., 1969, p. 37f. |
| 4. | Encyclopaedia Britannica, 14th ed., v. 8, p. 57. |
| 5. | Ibid. |