METROLOGY AND CHANCE

by Robert Forrest

In my previous article on metrology (J. Geomancy 1/4) I showed by practical example how metrological relationships could arise quite by chance, and to an intuitively surprising degree. As A.J .Bell pointed out, spurious metrology actually dealt me an unsuspected blow (J. Geomancy 2/1, p. 18), so that even mathematicians are susceptible to the tricks of chance! The present article, largely in response to A.J. Bell’s closing remark, concerns the formulae for evaluating how many metrological relationships of various types can arise purely by chance in a (for simplicity’s sake) rectangular area of country, amongst a given number of sites. There are two types of metrological spacing, between ancient sites, which are commonly sought, and these require quite different formulae.

CASE 1

Here the metrologist seeks evidence that sites are separated by some unit of measurement or ITS MULTIPLES. For example, he might be considering the use of the megalithic mile (2·72 miles), and so he searches for sites which are 1, 2, 3 or 4 etc. megalithic miles apart.

A certain amount of error is usually tolerated in such researches, and this tolerance needs to be known to evaluate the chance expectation figures. For example, our metrologist might decide that two sites separated by anything between 2·71 miles and 2·73 miles is an intended megalithic mile, possibly distorted by a small builder’s error, as it were. In such a case we define our metrologist’s tolerance, e, to be 0·01 miles, since he is allowing errors up to 0·01 miles either side of the ‘intended’ megalithic mile. Similarly, 5·44 ± 0·01 miles counts as 2 megalithic miles, 8·16 ± 0·01 miles counts as 3 megalithic miles, and so on.

For a rectangular area of country, or map, of dimensions a × b, containing n sites, and in which we are seeking inter-site distances which are whole-number multiples of some unit u, to a tolerance ±e, then it is not too difficult to show that PROVIDED (a) u is small compared with the dimensions of the area under consideration, say, less than about 1/3 of the smaller of a and b, and (b) e is small compared with u, say, e is less than about 10% of u, then we can expect:

n(n − 1) e

u

inter-site distances which are, to within the given tolerance limit, whole-number multiples of u in value.

EXAMPLE: On a complete 1:50 000 O.S. sheet there are 185 sites. How many inter-site distances can I expect to be whole numbers of megalithic miles, with tolerance e = 0·01 miles?

2·72 miles = 4·38 km, and a 1:50 000 sheet 40 km × 40 km, so that a megalithic mile (u) is certainly under 1/3 of the map edge. Substituting the formula: e = 0·01, u = 2·72, n = 185, we have:

(185 × 184 × 0·01)	= 125
2·72

inter-site distances to be multiples of the megalithic mile. (Note: if u is larger than about 1/3 of the lesser side of the rectangle, the above method becomes inaccurate. The method required for such cases is cumbersome, and is omitted here).

CASE 2

Here, the metrologist is interested in a unit but not its multiples. For example, he might be interested in sites separated by 9 km, but not multiples of 9 km (18, 27, 36 km etc.).

Again, for chance expectation purposes, we need to know the tolerance, ±e allowed in the search for inter-site distances of the unit u.

The formula here is rather more complicated. For a rectangular area, a × b, containing n sites, in which we are searching for sites separated by distance u ( but not 2u, 3u, 4u etc.) to a tolerance ±e, then the chance expectation score of such inter-site distances is:

2n(n − 1).e.(πabu − 2(a + b)u² + u³)

a²b²

where π = 3·1416. This formula holds good PROVIDED (a) e is less than about 10% of u, and (b) u is less than or equal to the smaller of a or b.

{67}

EXAMPLE. On a 1:50 000 O.S. sheet containing 164 points I am searching for sites separated by a unit of 2 miles (but not multiples thereof). Allowing a tolerance of up to 0·05 miles either way, what is the chance expectation number of such inter-site distances?

Firstly, converting everything to km (a, b and u and e must of course be expressed in the same units), we have a = b = 40 km, u = 2 miles = 3·219 km, e = 0·05 miles = 0·0805 km, and n = 164. Substituting the formula, the chance expectation score is:

2 × 164 × 163 × 0·0805 × (3·1416 × 40 × 40 × 3·219 − 2 × 80 × 3·219² + 3·219³)

40² × 40²

=	4303·9 (16180 − 1658 + 33)	= 24·5
	2 560 000

Radial Systems

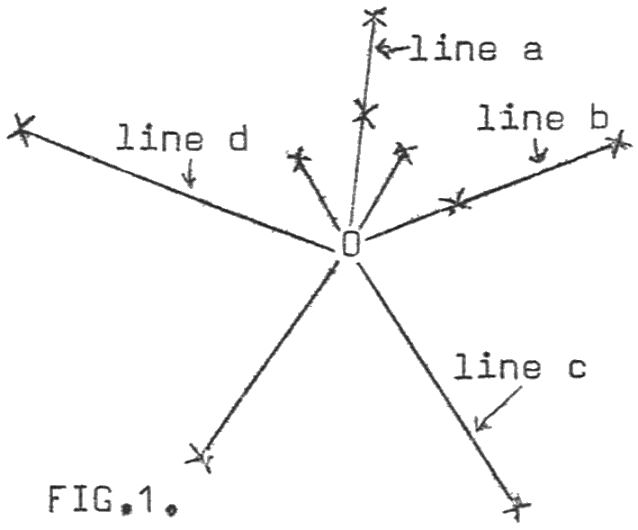
So far we have considered cases where the metrologist approaches his map, on which are a number of sites, and proceeds to test the distances between more or less any pair of these sites for the ‘use’ of some unit of measurement. The present case, that of a radial system (see Fig 1), is where the metrologist is concerned with distances from some central point, O, which may be an important site (e.g. Stonehenge, Glastonbury Abbey) or perhaps the centre of a terrestrial zodiac, to other ancient sites which surround it. The metrologist is thus concerned solely with the distances from O, rather than between pairs of sites which surround O. These surrounding sites may lie on alignments through O, such as lines a and b, or they may not, as in the case of lines c and d. The question again is: what can chance alone produce in such a situation?

Given a centre point O, and n surrounding sites, and supposing that we are searching for sites whose distances from O are whole number multiples of some unit u, each to tolerance ±e, then the chance expectation number of ‘hits’ is 2ne/u where, as in case 1, u is less than about a third of the smaller map edge, and e is less than about 10% of u.

EXAMPLE. Suppose the hypothetical example-map of case 1 possessed a terrestrial zodiac centre. Hew many of the surrounding 185 sites would, by chance, happen to be whole numbers of megalithic miles from that centre? Allowing a tolerance of ±0·01 miles, as before, the formula gives:

2 × 185 × 0·01	= 1.4 distances.
2·72

A note on the counting of sites, `n`.

If, to take a simple example, we are concerned with distances between standing stones, then, in the formulae quoted above, n must be the total number of standing stores in the area under study and not simply the number of standing stones between which distances in terms of the unit u have already been found.

Similarly, in considering, say, distances between a mixture of stones, stone circles, barrows and tumuli, then n must be the sum total of all such classes of sites in the area studied, and again not simply the number of such sites which have provided the ‘evidence’.