Notes on the Furness formula

Michael Behrend (2014)

The Furness formula, which estimates how many alignments of ancient sites might occur by chance, was published by Peter Furness in an article in The Ley Hunter in 1965. He seems to have used as his starting-point an article by Donald H. Menzel which appeared in Flying Saucer Review in the same year, and which tackled a similar problem for UFO sightings.

The Menzel–Furness method uses a strip criterion: that is, for a set of points to be considered aligned it is necessary that they can be covered by a narrow strip of width x, where x (called the strip width, ley width, or corridor width) is specified in advance.

Neither Menzel nor Furness makes it entirely clear whether, in addition, the centre line of the strip is assumed to pass through two of the points. If this is assumed, we may call the criterion for alignment the “centred strip” criterion; if not, the “free strip” criterion. Bob Forrest’s discussion in The Linear Dream assumes a centred strip. Indeed, another of Menzel’s articles in Flying Saucer Review (March/April 1964, p. 5) does define the corridor in such a way that two of the points are on the centre line. On the other hand, the Furness formula agrees better with computer simulations carried out with a free strip criterion (see below). This made me think for a time that Menzel was using a free strip criterion. However, I am now satisfied that (as explained below) Menzel’s method is fallacious, and that the reasonable agreement with computer simulations for the free strip criterion is a fluke. If Menzel did have a centred strip criterion in mind then the Furness formula, based on Menzel’s arguments, is badly in error.

Furness’s contribution

Furness improved on Menzel by giving a theoretical estimate of W, the expected total number of alignments (including 2-point lines). Namely, from Menzel’s equations (9):

W=	(	n	)	−	∑	ⁿ	(m−2)(m+1)	N°(m)
		2				_m₌₃	2

(A)

and (4):

N(m)=WP(n,m)

(B)

and his remark “If the observed distribution is random, we should expect N(m) to equal N°(m)”, it follows that we can put N°(m)=WP(n,m) in equation (A) and, with a bit of rearranging, get an estimate of W independent of the N(m). It seems that Menzel did not notice this, because in his method W is calculated from the alignment counts N(m) in each particular case.

The expression for W that Furness derives in this way is his equation (3). It can be simplified, in that the sum in the denominator can be found explicitly. The denominator is

1+	∑	ⁿ	[(	m	)	−1	]	P(n,m)
		₃		2

where

P(n,m)=	(	n−2	)	ƒ^m⁻²(1−ƒ)ⁿ^−m.
		m−2

(C)

Although the denominator appears at first sight to contain powers of ƒ up to ƒⁿ⁻², it turns out that terms in ƒ³ and upwards cancel out, leaving the denominator as

1+2(n−2)ƒ+½(n−2)(n−3)ƒ².

(Bob Forrest independently noticed such a simplification in Appendix 1 of The Linear Dream.) Multiplying numerator and denominator by 2, we can therefore rewrite Furness’s equation (3) as

W=	n(n−1)	.
	2+4(n−2)ƒ+(n−2)(n−3)ƒ²

(D)

Fallacies in the method

When Menzel’s article is read critically, it is difficult to follow his reasoning. Yet his method gives results close to the truth for the free strip criterion, at least when the ley width is very small. After puzzling over his method for some time, I have come to the conclusion that it contains two fallacies, which happen to cancel each other out.

Consider the simplest non-trivial case, that of three points placed randomly (independent uniform distributions) on the map. What is the probability that they are aligned?

Recall that Furness defines N(3) as the number of 3-pointers and W as the total number of alignments (including 2-pointers). In our example there are only two possibilities: either the three points are aligned, in which case N(3)=1 and W=1, or they are not aligned, in which case N(3)=0 and W=3. These possibilities, taken together, are inconsistent with the Menzel–Furness equation (B), which here becomes

N(3)=WP(3,3)

(E)

where P(3,3) is independent of how the points are placed.

To avoid this difficulty it may be said: consider the mean values of N(3) and W when the experiment is repeated many times. Let the probability of alignment be q, and note that equation (C) gives P(3,3)=ƒ. Replacing W and N(3) in equation (E) by their mean values we get

q=(3−2q)ƒ

whence q=3ƒ/(1+2ƒ), which is correct to order ƒ and identical with the value obtained from the Furness formula.

But this still will not do. To see why, it may be helpful to replace the map area by a finite affine plane. Recall (see e.g.Wolfram MathWorld) that an affine plane of order k has k² points with k points on every line. Such a plane exists whenever k is a prime power, so we will suppose here that k is large. We can now do away with the “ley width” and identify corridors with exact straight lines, while keeping non-zero probabilities. The probability ƒ that a point chosen uniformly at random lies in a given corridor is now given by

ƒ=k/k²=1/k.

The probability that a random set of three distinct points, all such sets being equally likely, forms an alignment is (k−2)/(k²−2), and this can be made arbitrarily close to ƒ by taking k large enough. But Menzel’s argument goes through as before and tells us that the probability of alignment is close to 3ƒ.

With this hint the fallacy becomes clear. Consider how Menzel’s set of W corridors is obtained. In the rare case that the points are aligned, we add one 3-pointer to the set. If the points are not aligned, we add three 2-pointers to the set. We are then asked to estimate the number of 3-pointers as if the W corridors had been chosen at random. Clearly this will give a result about 3 times the correct value.

The other fallacy is easier to spot. Menzel writes “We use any pair of corridor points to fix the corridor.” But with the free strip criterion two points do not fix the corridor absolutely. The corridor can move about somewhat while continuing to cover the points. Thus the fraction of the map area available for a third point to align with the first two is not ƒ but something larger. If the calculation is done properly the probability that three random points are aligned is found to be 3ƒ. This, by a fluke, is the value that Menzel derived by the fallacy discussed above.

If Menzel was thinking of a centred strip criterion, then the position of the strip is still not absolutely fixed. A centred strip can be moved so as to make an alignment In the diagram (left) the first two points A, B define a strip, and the third point C falls outside the strip; but if the centre line is made to pass though A and C instead (right), the point B is still inside the strip. Because the order in which the points are placed is immaterial, ABC counts as an alignment. With this criterion the probability that three random points are aligned is not ƒ but 3ƒ/2, and the Menzel–Furness method predicts twice as many 3-pointers as actually occur (see simulation results below).

Another difficulty is with the estimate of W, the total number of alignments including 2-pointers. Furness, following Menzel, uses:

(

)

−

∑

ⁿ

[(

)

−1

]

N(m)

₃

(F)

where N(m) (m≥3) is the number of m-point alignments. The reasoning seems to be: two points determine an alignment, so start with the number of point-pairs; but then an m-pointer (m≥3) will be counted ( m 2 ) times instead of once, so reduce W accordingly. What this reasoning overlooks is that a pair of points may occur in more than one alignment. In the diagram, n=4, N(3)=2, and N(4)=0, so equation (F) gives W=2; but in fact W=3. 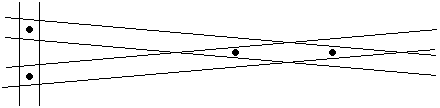Two 3-pointers share a pair of points I think this is why the Furness formula tends underestimate the number of alignments expected with the free strip criterion. When the ley width is very small, the formula is close to the truth; but as the ley width increases, the sharing of point-pairs as in the diagram also increases, and the estimate of W becomes too small.

Comparison with simulations

The following table shows the number of 3, 4, and 5-pointers found among 30 points in a square of side 1, for various values of the ley width x. As one would expect, the number of alignments with the centred strip criterion (in which the centre line of the strip is required to pass through two of the points) is much less than with the free strip criterion (in which this condition is not imposed). The table shows the average number of alignments found in 10 000 000 computer simulations.

The table also shows the expected number of alignments calculated by the Furness formula. It can be seen that the Furness value agrees better with the free strip than with the centred strip.

		x=0.0001		x=0.0002		x=0.0005		x=0.0010
	Centred strip	0	.63	1	.26	3	.12	6	.1
3-pointers	Furness	1	.26	2	.50	6	.08	11	.7
	Free strip	1	.26	2	.51	6	.17	12	.0

	Centred strip	0	.00067	0	.00269	0	.0165	0	.065
4-pointers	Furness	0	.00177	0	.00703	0	.0428	0	.164
	Free strip	0	.00183	0	.00723	0	.0447	0	.174

	Centred strip	0	.000000	0	.000004	0	.000067	0	.00053
5-pointers	Furness	0	.000002	0	.000013	0	.000194	0	.00149
	Free strip	0	.000002	0	.000013	0	.000202	0	.00165

Comparison with the strip formula

Elsewhere on this website can be found details of the strip formula, which I wrote up in 1977. This gives the expected number of alignments in a set of random points under a free strip criterion, when a set of points is considered aligned if and only if they can be covered by a strip of pre-defined width 2c. It’s assumed that c is small compared with the size of the map, as is the case in ley hunting. Computer simulations confirm that the formula is accurate for small c.

An important difference between the strip formula and the Furness formula is that the strip formula counts all alignments of a given order, even if they are contained in alignments of greater order. For instance, a 5-pointer ABCDE would be considered to contain also 5 4-pointers (ABCD, ABCE, etc.) and 10 3-pointers (ABC, ABD, etc). The Furness formula, on the other hand, counts only maximal alignments, so that e.g. a 4-pointer contained in a 5-pointer would not be counted.

This difference of definition means that the Furness formula and strip formula cannot be compared in general. There are, however, two cases where this can be done: (a) Given a (small) number of points placed at random on the map, find the probability that they are all aligned; if they are, then the alignment is obviously maximal. (b) Consider what happens as the ley width (x or 2c) tends to 0; for a very small ley width almost all alignments will be maximal.

In both these cases it is found that the Furness formula and the strip formula essentially agree. From the 1977 notes on the strip formula we have that the expected number of r-point lines (maximal or not) when n points are placed randomly on the map is

e(n,r)=	n!	⋅	2^r⁻⁴r(r+1)	⋅M_r₋₂(c/A)^r⁻²
	(n−r)!		3(r−2)!

where A is the area of the map and M_r₋₂ is the (r−2) moment of the distance between two randomly placed points.

For comparison with the Furness formula, we need to put c=x/2 and, less trivially, use the theorem proved elsewhere on this website that M_r₋₂ is related to the (r−2) moment of the chord length, say L_r₋₂, by

L_r₋₂=	r(r+1)	M_r₋₂.
	6

A simple calculation now gives

e(n,r)=	n(n−1)	(	n−2	)	(	x	)	^r⁻²	L_r₋₂.
	2		r−2			A

For case (a) above, let m points be placed randomly on the map. The probability that they are aligned is, according to the strip formula,

e(m,m)=	m(m−1)	(	x	)	^m⁻²	L_m₋₂
	2		A

and according to the Furness formula

m(m−1)	(	xy	)	^m⁻²
2+O(ƒ)	(	A	)

where y is the vaguely defined “length of a typical ley”. Since ƒ is small, the fomulae essentially agree provided we allow that y^m⁻²=L_m₋₂ , which seems reasonable (although it makes y vary somewhat with m).

For case (b) above, consider the number of m-point lines when there are n points on the map and the ley width x tends to 0. Recalling that Furness defines ƒ=xy/A, take x so small that nƒ is small. Then (1−ƒ)ⁿ^−m is close to 1, and so from equations (B), (C) and (D) we find that the expected number of m-point lines N(m) is close to

n(n−1)	(	n−2	)	(	xy	)	^m⁻²	.
2		m−2			A

This is the same as e(n,m) of the strip formula provided that, as in case (a), we identify y^m⁻² and L_m₋₂.