Unit 3: Floating-point numbers

Introduction

Haskell has two types for floating-point numbers, namely Float (single-precision) and Double (double-precision). Floating-point numbers can be represented in two ways. First, using a decimal point:

2.0
33.873
-8.3377

Second, by means of the so-called scientific notation:

33.61e6
3.7e-2
-3.7e2

These are equivalent to the following, in order:

33.61*106
3.7*10-2
-3.7*102

Haskell has the usual binary infix floating-point operators, namely + (addition), - (subtraction), * (multiplication), / (division) and ** (exponentiation). It has the unary prefix operator - (minus or negative) and the constant pi is also defined. There are several useful unary prefix operators available:

Note that the arguments to the trigonometric functions are taken to be in radians: π radians are the same as 180 degrees.

Haskell has some useful functions for converting floating-point numbers into limited-precision integers, namely ceiling 2.3 which is equivalent to 3, floor 2.3 which is equivalent to 2 and round 2.3 which is equivalent to 2. Note that round 2.7 is equivalent to 3. These are all of type Float -> Int.

Numerical type classes

So far four numerical types in Haskell have been introduced, namely Int, Integer, Float and Double. It is tedious to define a new function that squares its argument, say, for each numerical type:

sqInt :: Int -> Int
sqInt x = x * x

sqInteger :: Integer -> Integer
sqInteger x = x * x

sqFloat :: Float -> Float
sqFloat x = x * x

sqDouble :: Double -> Double
sqDouble x = x * x

Haskell has several type classes which allow one definition to do the work of more than one of the above monomorphic definitions:

sqIntegral :: Integral a => a -> a
sqIntegral x = x * x

sqFractional :: Fractional a => a -> a
sqFractional x = x * x

sqReal :: Real a => a -> a
sqReal x = x * x

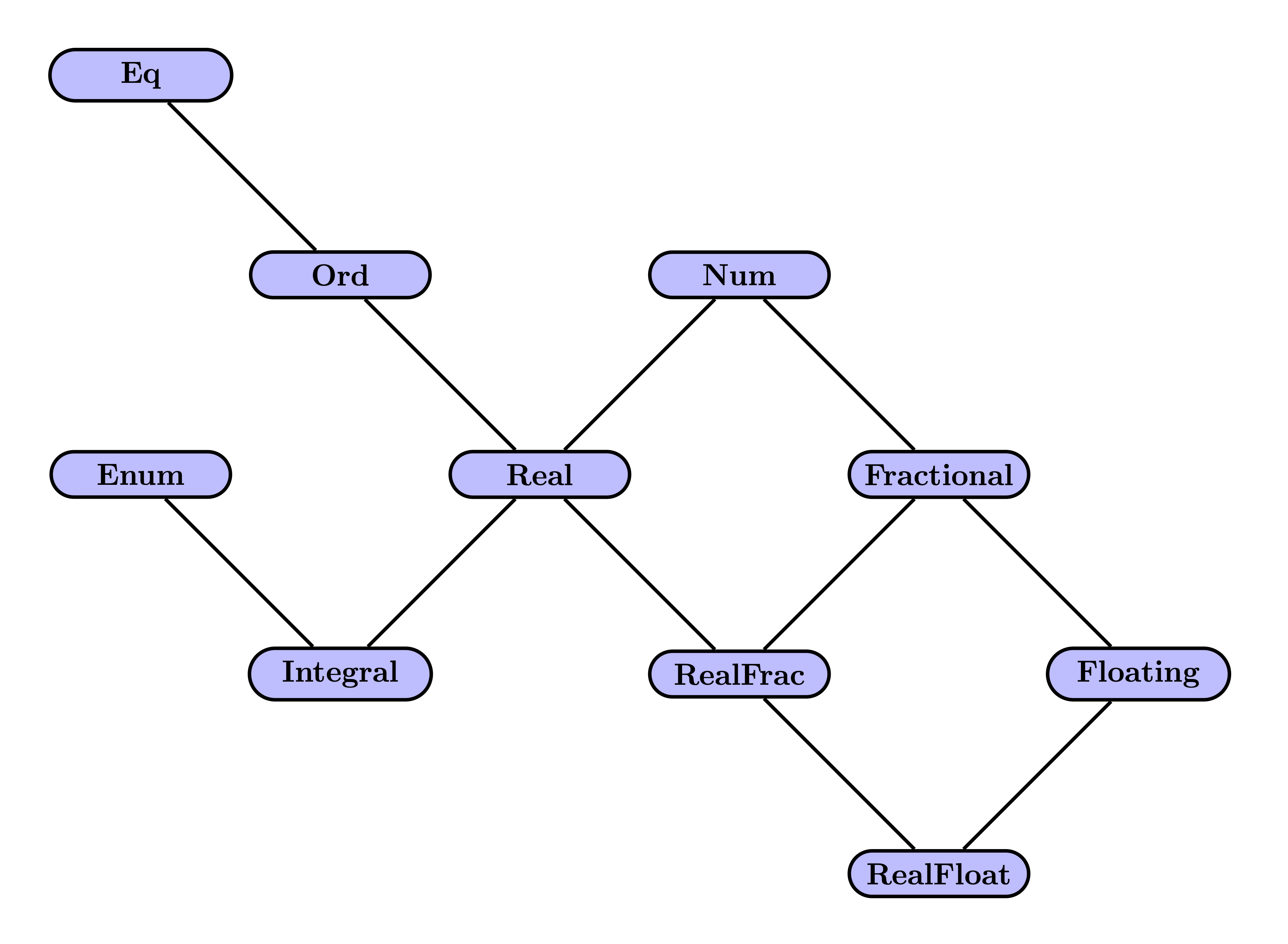
The type class Integral contains the types Int and Integer. The type class Fractional contains the types Float and Double. The type class Real contains the types Int, Integer, Float and Double. These, and some other important type classes are shown in Fig. 1, but note that Haskell has many more type classes. One of the differences between the language defined in the Haskell Report and that implemented by the GHC is that the GHC does not consider Eq to be a superclass of Num.

Characters

The type Char contains characters. Elements of Char are written enclosed in single closing quotation marks, for example: 'a', 'B', '4', '\t' (tab), '\n' (newline), '\\' (backslash), '\'' (single closing quotation mark) and '\"' (double quotation mark). The single opening quotation mark is simply written between single closing quotation marks, thus '`'.

There are many useful functions defined on characters contained in the library Data.Char. To use these you have to import this module. The functions toUpper and toLower, both of type Char -> Char, do what you would expect. The function ord, of type Char -> Int, turns a character into its ASCII code. The function chr, of type Int -> Char, turns an ASCII code into a character.

There are also several Boolean-valued functions defined on characters available in Data.Char. Some of these are: isAscii, isUpper, isLower, isAlpha, isDigit and isAlphaNum.

© Antoni Diller (23 September 2021)