
Translated from “Le jeu des labyrinthes”,
E. Lucas, Récréations mathématiques, vol. I (2nd edn, Paris, 1882), ch. 3, pp. 41–55.
This chapter of Lucas’s classic work first surveys briefly the history of mazes and labyrinths, and then describes Trémaux’s algorithm for solving a maze. Finally there are some graph-theoretical notes on trees.
{41}
Reader, suppose you are lost amid the junctions of a maze, in the galleries of a mine, in the tunnels of the catacombs, beneath the shady rides of a forest. You have no Ariadne’s thread, in your hand, and you are in the same position as Tom Thumb [8], after the birds had eaten the breadcrumbs sown along his route. How can you find the exit of the maze, the shaft of the mine, the entry to the catacombs, the woodman’s cabin? This recreation will teach you that a lost way can always be found.
Ancient authors regarded labyrinths as inextricable, a prejudice that is perhaps still with us. This name was given to buildings composed of alleys or galleries whose innumerable ramifications made it impossible for the visitor to leave. The works of antiquity are full of descriptions of these wonderful monuments which were used as tombs, and of which there remains almost no trace today. In Egypt, there were two of them: the labyrinth of Mendes, located in the island of lake Mœris, and that of the Twelve Kings, built to the south-east of the same lake, by Psammetichus, almost seven centuries before the Christian era. Pliny reports that it was a monument dedicated to the Sun; it was composed of a series of temples connected or superimposed one on the other, covering an extraordinary area; the streets formed inextricable circuits and turnings.
But, of all these monuments, that which was most sung by the poets is the Cretan labyrinth, built by order of king Minos, to be used as prison for the Minotaur:
When Minos, willing to conceal the Shame
That rose from the Reports of tatling Fame,
Resolves a dark Inclosure to provide,
And, far from Sight, the two-form’d Creature hide.
Great Dædalus of Athens was the Man
That made the Draught, and form’d the wondrous Plan;
Where Rooms within themselves encircled lye,
With various Windings, to deceive the Eye.
As soft Mæander’s wanton Current plays,
When thro’ the Phrygian Fields it loosely strays;
Backward, and forward rolls the dimpl’d Tide,
Seeming, at once, two different Ways to glide;
While circling Streams their former Banks survey,
And Waters past succeeding Waters see:
Now floating to the Sea with downward Course,
Now pointing upward to its ancient Source.
Such was the Work, so intricate the Place,
That scarce the Workman all its Turns cou’d trace;
Th’ ambiguous Ways it’s Artist scarce could find
Lost in the Mazes of his own Design.
(Ovid, Metamorphoses, book VIII) [9]
The idea of inextricability appears in this passage from Ovid, the translation of which has at least the merit of giving, by the number of epithets, some idea of the multiplicity of junctions in the labyrinth. One finds idea again in the Lettres à Émilie by Demoustier: “This immense building, he says, contained an infinity of circuits contrived with treacherous skill:
Hélas! il ressemblait au cœur de l’infidèle,
Dont l’innocence ignore les détours;
Sans le savoir, on s’engageait comme elle,
On se perdait comme elle pour toujours.
Perhaps there is in all this merely a poetic legend; no author of antiquity says he has seen this labyrinth; by the time of Diodorus and Pliny, there were no longer any external traces of them to be found. However, there still exist in the island of Crete several caves with covered galleries, which Cretans do not hesitate to recognize as the remains of the labyrinth entered by the beautiful Ariadne, daughter of Minos.
The famous botanist Tournefort visited, about 1702, one of these caves, hollowed at the foot of Mount Ida. In his letters to the Minister Pontchartrain, published under the title Voyage du Levant, he relates that after having wandered some time through a network of underground corridors, the explorers arrived at large and broad avenue which led them to a very fine hall, located at the bottom of the labyrinth. “We made, he says, in the space of half an hour 1460 paces in this principal alley without deviating either to right or left. It is seven feet high, panelled with a horizontal layer of rocks and quite flat, as are most of the stone-beds of this district. There are however some places where you need to duck your head a little, and one, among the others, to be met with about half way along, where you are obliged, as they say, to go on all fours. This alley is mostly wide enough to let two or three people pass abreast. The paving is level; there is no need to step any considerable distance up or down. The walls are cut vertically, or are made from stones which obstructed the way, and which have been arranged with painstaking neatness, as is done in walls where mortar is not used; but so many paths present themselves on all sides, that one would undoubtedly lose oneself there without the necessary precautions. Since we greatly desired to find our way out, we posted: (1) one of our guides at the entrance to the cave, with orders to fetch people from the nearest village to come and rescue us, supposing we had not returned by nightfall; (2) each of us carried a torch in his hand; (3) we attached numbered papers on the right-hand side of all turnings which appeared to us difficult to retrace; (4) one of our Greeks placed on the left small bundles of thorns of which he had brought a supply, and another took care to sow on the way the straw which he carried a bag under his arm.”
There still exist the ruins of several other labyrinths: in Lemnos, Agrigentum, Clusium. As to this last building, which was used as burial-place of Porsenna, we have the testimony of Marcus {45} Varro, quoted by Pliny: Its base contained an inextricable labyrinth; if anybody entered there without a ball of thread, he could not find the way out. This building, adds Pliny, was a monument to human folly and vanity.
In the Middle Ages, the labyrinth becomes a specific style of paving in Gothic churches. The arrangement, shape and colour of the tiles combine to form sinuous lines leading by many meanders to various stations, and finally to an image of Calvary. Among the best-known labyrinths of this kind, on which people carried out miniature pilgrimages, must be mentioned those in the cathedrals of Amiens, Sens, Rheims, Chartres, Bayeux; these last two still exist, as does that of the collegiate church of Saint-Quentin.
In Paris today we still have two labyrinths, not counting the maze of our streets, boulevards and sewers: that of the old quarries, beneath the left bank of the Seine, and that of the Jardin des Plantes. By special permission, the public can visit part of the former, which is known as Ossuary of the Catacombs; it contains the remains of burials in the old cemeteries. One cannot get lost in it, because the visitors, counted at the entry and exit, follow one another in procession, guided by a broad black trail, a kind of Ariadne’s thread, that the smoke from the candles has traced on the roof of the quarries. As for the labyrinth of the Jardin des Plantes, it is, on sunny days, a meeting place for the children who run and hide in the circular alleys, which are bordered by fir trees and rockeries and shaded by large cedars.
{46}
We can regard the junctions of a labyrinth as geometrical points; the alleys, corridors, streets, galleries, as straight lines or curves, plane or three-dimesional, each joining two of these points. We will say that these points and lines form a geometrical network or a labyrinth when a mobile point placed on one of the lines of the network can pass to any another point, without leaving the lines of the system. On that assumption, we will show that this mobile point can successively describe all the lines of the network, without sudden jumps, and without passing more than twice over any of them. In other words, a labyrinth is never inextricable.
You can make a game in the following way: Choose at random on a sheet of white paper any number of points; join them two by two as many times as you like by any number of lines, straight or curved, in such a way no point of the system remains isolated from the rest; you then have a geometrical network. Draw, for example, the network of bus and tram routes of a large city, the rail network of a country, the network of rivers, streams and canals of any district, adding, if you like, the coasts and frontiers.
The drawing is to be covered an opaque piece of cardboard, so as not to remind you the plan of the labyrinth; this sheet of cardboard is pierced with a hole which we will call an eyepiece, and which only allows you to see a small fraction of the network. The cardboard or screen is moved so {47} that the eyepiece is placed on a junction A. The task is to make all lines of the network twice pass twice through the eyepiece, in a continuous manner, returning finally to the starting point A. To record the passage of the eyepiece over each path that it traverses, every line followed is marked with a small cross-stroke on entering and leaving the junctions. Consequently, the two ends of each path must, when the wandering journey is over, be marked twice and no more.
In a real labyrinth, or the gallery of a mine, a walker who is lost will deposit a mark, a stone, on entering and leaving each junction, in the alley which he has just left and the one he has just entered.
Among the various solutions to this curious problem in the geometry of situation, the statement of which we have just given, we will choose, as the simplest and most elegant, the one that was kindly communicated to us by M. Trémaux, a former student of the École Polytechnique, now a telegraph engineer; but we have slightly modified the proof.
First rule. – On leaving the initial junction, follow any path, until you arrive at a dead end or a new junction: (1) if the path you have followed leads to a dead end, retrace your steps, after which you may consider the path just taken as removed, since it has been traversed twice; (2) if the path leads to a junction, take {48} any path [10], at random, being careful to mark a cross-stroke on the entrance path in the direction of the arrow f, and on the exit path in the direction of the arrow g (fig. 9). In this figure and the three following, we have distinguished old marks from the new ones by adding to the latter a small cross.
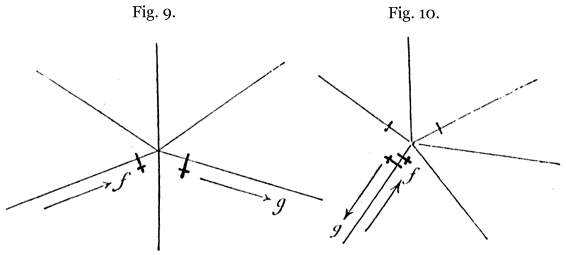
Keep applying the first rule, each time you arrive at an unexplored junction; after a time you will necessarily arrive at a junction that has already been explored; but this situation can arise in two different ways, according as the path into that junction has been followed once before or is still unmarked. Then you apply one of the following two rules:
Second rule. – On arriving at an already explored junction by a new path, you must turn back, adding two cross-strokes to mark your arrival at the junction and your departure, as shown in fig. 10.
Third rule. – When you arrive at an already explored junction by a path that has already been followed, take as your first choice {49} a path that has not already been traversed, if there is one; failing that, a path which has been traversed only once; these two cases are shown in fig. 11 and 12.
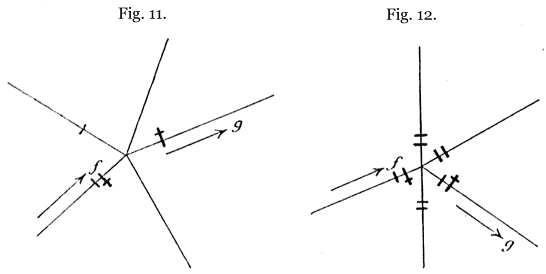
Proof. – By a strict application of the above rules, you will necessarily traverse twice all the lines of the network. First let us make the following remarks:
I. On leaving the junction A, only one initial mark is introduced there.
II. Passing through a junction, by using one of the three rules, adds two marks to the lines which end at that junction.
III. At any time during the exploration of the labyrinth, before arrival at a junction or after departure from a junction, the initial junction contains an odd number of marks, and any other junction contains an even number.
IV. At any time during the exploration, before or after passing through a junction, the initial junction can have {50} only one path with a single mark; any other explored junction can have only two paths with a single mark.
V. When the exploration is finished, all the junctions must be covered with two marks on each path; this is the condition imposed by the statement of the problem.
After these remarks, it is easy to see that, when the traveller arrives at a junction M different from the initial junction A, he cannot be stopped in his tracks by the difficulties of the problem. For this junction M can be reached only by a new path, or a path that has been traversed only once before. In the first case, one applies the first or the second rule; in the second case, arrival at the junction produces an odd number of marks; thus, in view of Remark III, there remains, in the absence of a new path, a line which has been traversed only once.
Thus, the only place where you can be stopped is on return to the initial junction A. Let ZA be the path that leads to a forced halt, coming from junction Z; this path has necessarily been traversed once already, since otherwise one could continue the journey. Since the path ZA has already been traversed, there is no path in the junction Z that has never been traversed at all, since otherwise you would have forgotten to apply the first case of the third rule; moreover, there was apart from ZA one path, and only one, YZ, traversed only once, in view of Remark IV. Consequently, at the time of the halt at A, all the paths of junction Z have been traversed twice; it can be shown, in the same way, that all paths of the preceding junction Y have been traversed twice, and so on for the other junctions. This is what had to be proved.
{51} Remark. – One can replace the second rule by the following, when it is not a question of a closed junction. If you arrive, by a new path, at an already explored junction, you can take a new path, provided you label the two cross-strokes, that mark your passage through the junction, with matching indices a and a′; then, if you return to the junction by one of these two paths, one you must take the other. This amounts, so to speak, to placing a bridge aa′ over the junction. This rule was pointed out to us by M. Maurice, former student of the École Polytechnique.
We saw that, in the applying the second rule, we must turn back when we arrive, by a new path, at an explored junction. Let us suppose that we remove, in the network, a small piece of the path that ends at this junction, and that we carry out the same operation at all places where we turn back; the network is then changed into another geometrical figure variously known as a tree, ramification, arborescence; the ways take the name of branches, and the junctions the name of forks or nodes. Similar configurations have been studied by MM. Sylvester, Cayley, Septimus Tebay, and quite recently by Prince Camille de Polignac (1).
(1) Jordan, Journal de Borchardt. – Sylvester, Educational Times. – Cayley, British Association Report, 1875. – De Polignac, Bulletin de la Société mathématique, t. VIII, p. 120.
A geometrical tree is usually defined {52} as follows: From each node one can, by following the branches, arrive at any other node, but by only one route. This theory has been considerably simplified by M. de Polignac by means of a fundamental remark. To explain: any tree can be traced by means of a certain number of continuous routes, without repetition or stopping; that is, by starting at the end of a branch and continuing until one arrives at the end of another branch or at an already traversed branch. Note that the route is required to cross a line, even though that line has already been traced, if it can keep going without travelling along the line. Given that definition:
Fundamental remark. – No matter how a tree is traced without repetition or stopping, the number of routes will always be the same.
To prove this, let us make a cut across every branch that joins two nodes; this will break up the tree into a series of stars. We shall rebuild the tree by restoring the common rays to the stars. For each star, taken by itself, the fundamental property is obvious. Let us denote by N1, N2, N3, …, Np, the number of rays belonging to each star; by p the number of nodes or stars. If the first two stars are now joined together, we lose one route from the total number over all stars; joining the second star to the third, we lose yet another route; so that finally, if N denotes the number of routes that were used to trace the tree, we have
| N = N1 + N2 + N3 + … + Np − (p − 1) . |
We will call the number N the basis of the tree; one {53} can express the numbers N1, N2, …, and consequently the number N itself in terms of the order of the nodes, or stars, i.e. by the number of branches or rays which end there. The simplest node is the ternary or third-order node; if, in general, mq is the order of a node one has firstly m at least equal to three; the number Nq of routes which make it possible to draw this node is equal to half of mq, if mq is even, and equal to half of mq + 1, if mq is odd; it is thus, in each case, the greatest integer contained in the fraction (mq + 1) /2.
This number is usually represented by the symbol
| [ | mq + 1 | ] | ; |
| 2 |
consequently the preceding formula can be written
| N = | [ | m1 + 1 | ] | + | [ | m2 + 1 | ] | + … + | [ | mq + 1 | ] | − (p − 1) . |
| 2 | 2 | 2 |
In this way one can determine the basis of the tree by knowing the number and orders of the nodes.
Let us denote by l the number of free ends of the branches, and suppose that the tree has only third-order nodes; we have then, however many third-order nodes there are, the formula
| N = l − 1 . |
This formula is obvious for a star with three rays; if one adds a third-order node at the free end of a branch, one replaces this end by two others, and one adds a route; when one forms a ternary node by adding a twig to a branch, one adds a route and a loose lead. In both {54} cases, both sides of the preceding formula increase by 1. Thus this formula is general.
In general let us indicate by pk the number of nodes of order k; we have, for two separate fourth-order nodes ( p′4 and p″4 being 1),
| N′ = l′ − 1 − p′4 , N″ = l″ − 1 − p″4 . |
On joining together two fourth-order nodes by a common end, the total number of routes decreases by 1, but two ends disappear; we thus have
| N + 1 = N′ + N″ , l′ + l″ = l + 2 , p′4 + p″4 = p4 ; |
consequently, we have for a tree with two fourth-order nodes
| N = l − 1 − p4 ; |
and this formula applies to a tree formed from any number of fourth-order nodes. Similarly it can be shown that the basis of a tree consisting entirely of p5 fifth-order nodes is given by the formula
| N = l − 1 − p5 . |
More generally, when a tree contains only nodes of order 2μ, we have
| N = l − 1 − (μ − 1)p2μ ; |
and when it contains only nodes of order 2μ + 1, we have again
| N = l − 1 − (μ − 1)p2μ + 1 . |
{55} Finally, by joining together two or more trees by two free ends, we obtain the general formula
| N = l − 1 − (p4 + p5) − 2(p6 + p7) − 3(p8 + p9) − 4(p10 + p11) − … . |
We will indicate in Note III at the end of this volume the various connections which one can establish between the theory of trees and the game of bridges and islands.