
E. Lucas, Récréations mathématiques, t. I (2ème éd., Paris, 1882), ch. 3, pp. 41–55.
This chapter of Lucas’s classic work first surveys briefly the history of mazes and labyrinths, and then describes Trémaux’s algorithm for solving a maze. Finally there are some graph-theoretical notes on trees.
{41}
Lecteur, supposez-vous égaré dans les carrefours d’un labyrinthe, dans les galeries d’une mine, dans les carrières des catacombes, sous les allées ombreuses d’une forêt. Vous n’avez point dans votre main le Fil d’Ariane, et vous êtes dans la situation du Petit Poucet, après que les oiseaux ont mangé les miettes de pain semées sur sa route. Que faire pour retrouver l’issue du labyrinthe, le puits de la mine, l’entrée des catacombes, la cabane du bûcheron? Cette récréation va vous apprendre que l’on peut toujours retrouver le chemin perdu.
Les anciens auteurs considéraient les labyrinthes comme inextricables; c’est peut-être encore un préjugé de nos jours. On {42} donnait ce nom à des édifices composes d’allées ou de galeries dont les innombrables ramifications mettaient le visiteur dans l’impossibilité de sortir. Les ouvrages de l’antiquité sont pleins de descriptions de ces monuments merveilleux qui servaient de tombeaux, et dont il ne reste presque plus de trace aujourd’hui. En Égypte, il y en avait deux: le labyrinthe de Mendès, situé dans l’île du lac Mœris, et celui des Douze Seigneurs, construit au sud-est du même lac, par Psammetichus, près de sept siècles avant l’ère chrétienne. Pline rapporte que c’était un monument consacré au Soleil; il se composait d’une série de temples reliés ou superposés les uns aux autres, occupant une étendue prodigieuse; les rues formaient des circuits et des détours inextricables.
Mais, de tous ces monuments, celui qui a été le plus chanté par les poètes, est le labyrinthe de Crète, construit par ordre du roi Minos, pour servir de prison au Minotaure:
Minos veut que dans l’ombre un vaste labyrinthe,
Prison du monstre affreux, le cache en son enceinte.
L’ingénieur Dédale, architecte fameux,
Traça les fondements de ses murs sinueux,
Et, dans de longs détours, sans terme et sans issue,
Par l’erreur des sentiers embarrassa la vue.
Tel qu’amoureux de suivre un tortueux chemin,
Le méandre se joue en son cours incertain,
Et vingt fois sur ses pas ramené dans sa course,
Se rencontre lui-même et retrouve sa source.
De détours en détours sur sa route égaré:
D’innombrables circuits par Dédale entouré,
Tel est le labyrinthe, et l’inventeur lui-même
Put à peine en sortir, tant son art est extrême!
(Ovide,
Métamorphoses, liv. VIII.) [9]
L’idée d’inextricabilité apparaît dans ce passage d’Ovide, dont la traduction possède au moins le mérite de donner, dans le {43} nombre des épithètes, une image de la multiplicité des carrefours du labyrinthe. On retrouve encore cette idée dans les Lettres à Émilie par Demoustier: « Cet édifice immense, dit-il, contenait une infinité de circuits ménagés avec une adresse perfide:
Hélas! il ressemblait au cœur de l’infidèle,
Dont l’innocence ignore les détours;
Sans le savoir, on s’engageait comme elle,
On se perdait comme elle pour toujours.
Peut-être n’y a-t-il dans tout cela qu’une légende poétique; aucun auteur de l’antiquité ne dit avoir vu ce labyrinthe; du temps de Diodore et de Pline, on n’en découvrait plus de vestiges extérieurs. Cependant il existe encore dans l’île de Crète (aujourd’hui Candie) plusieurs cavernes à galeries couvertes que les Candiotes n’hésitent pas à reconnaître pour les débris du labyrinthe où s’engagea la belle Ariane, fille de Minos.
Le célèbre botaniste Tournefort visita, vers 1702, l’une de ces cavernes, creusée au pied du mont Ida. Dans ses lettres au ministre Pontchartrain, publiées sous le titre de Voyage du Levant, il raconte qu’après avoir erré quelque temps à travers un réseau de corridors souterrains, les explorateurs arrivèrent à une grande et large avenue qui les conduisit à une fort belle salle, située au fond du labyrinthe. « Nous fîmes, dit-il, en une demi-heure de temps 1460 pas dans cette principale allée sans nous écarter ni à droite ni à gauche. Elle est haute de sept pieds, lambrissée d’une couche horizontale de rochers et toute plate, {44} comme le sont la plupart des lits de pierre de ce quartier-là. Il y a pourtant quelques endroits où il faut un peu baisser la tête, et un, entre les autres, que l’on rencontre vers le milieu du chemin, où l’on est obligé, comme on dit, de marcher à quatre pattes. Cette allée est ordinairement assez large pour laisser passer deux ou trois personnes de front. Le pavé est uni; il ne faut ni monter, ni descendre considérablement. Les murailles sont taillées à plomb, ou faites des pierres qui embarrassaient le chemin, et que l’on a pris la peine de ranger fort proprement, comme on fait celles des murailles où l’on n’emploie point de mortier; mais il se présente tant de chemins de tous côtés, que l’on s’y perdrait indubitablement sans les précautions nécessaires. Comme nous avions grande envie d’en revenir, nous postâmes: 1° un de nos guides à l’entrée de la caverne, avec ordre d’aller chercher du monde au village prochain pour venir nous délivrer, supposé que nous ne fussions pas de retour avant la nuit; 2° chacun de nous portait à la main un flambeau; 3° nous attachions sur la droite des papiers numérotés dans tous les détours qui nous paraissaient difficiles à pouvoir être repris; 4° un de nos Grecs laissait à gauche de petits fagots d’épines dont il avait fait provision, et un autre prenait soin de semer sur le chemin de la paille dont il portait un sac sous le bras. »
Il existe encore des ruines de plusieurs autres labyrinthes: à Lemnos, à Agrigente, à Clusium. On a sur ce dernier édifice, qui servit de sépulture à Porsenna, le témoignage de Marcus {45} Varron, cité par Pline: Sa base renfermait un labyrinthe inextricable; si quelqu’un s’y engageait sans peloton de fil, il ne pouvait retrouver l’issue. Cet édifice, ajoute Pline, était un monument de la folie et de la vanité humaines.
Au moyen âge, le labyrinthe devient une disposition particulière du pavage des églises gothiques. L’arrangement, la coupe et la couleur des pavés forment, par leurs agencements, des lignes sinueuses conduisant par de nombreux détours à différentes stations, et finalement à un calvaire figuré. Parmi les plus fameux labyrinthes de ce genre, sur lesquels on effectuait des pèlerinages en miniature, on doit citer ceux des cathédrales d’Amiens, de Sens, de Reims, de Chartres, de Bayeux; ces deux derniers subsistent encore, ainsi que celui de la collégiale de Saint-Quentin.
Aujourd’hui nous avons encore à Paris deux labyrinthes, sans compter le dédale de nos rues, de nos boulevards et de nos égouts: celui des anciennes carrières, sous la rive gauche de la Seine, et celui du Jardin des Plantes. Avec une autorisation spéciale, le public peut visiter la partie du premier, que l’on nomme Ossuaire des Catacombes; il renferme les débris des sépultures des anciens cimetières. On ne peut s’y égarer, car les visiteurs, comptés à l’entrée et à la sortie, se suivent processionnellement, guidés par une large traînée noire, sorte de fil d’Ariane, que la fumée des bougies a tracée sur la voûte des carrières. Quant au labyrinthe du Jardin des Plantes, c’est, aux jours de soleil, un lieu de réunion pour les enfants qui courent et se cachent dans les allées circulaires bordées de sapins et de rocailles, à l’ombre des grands cèdres.
{46}
Nous pouvons considérer les carrefours d’un labyrinthe comme des points géométriques; les allées, corridors, rues, galeries, comme des lignes droites ou courbes, planes ou gauches, réunissant ces points deux à deux. Nous dirons que ces points et ces lignes forment un réseau géométrique ou un labyrinthe lorsqu’un point mobile placé sur l’une des lignes du réseau peut passer à un autre point quelconque, sans quitter les lignes du système. Cela posé, nous allons démontrer que ce point mobile peut décrire successivement toutes les lignes du réseau, sans saut brusque, et sans passer plus de deux fois sur chacune d’elles. En d’autres termes, un labyrinthe n’est jamais inextricable.
Vous réaliserez un jeu de la manière suivante: Choisissez arbitrairement sur une feuille de papier blanc un nombre quelconque de points; joignez-les deux à deux et autant de fois que vous voudrez par un nombre quelconque de lignes, droites ou courbes, de telle sorte qu’aucun point du système ne reste isolé des autres; vous avez ainsi un réseau géométrique. Dessinez, par exemple, le réseau des lignes d’omnibus et de tramways d’une grande ville, le réseau des chemins de fer d’un pays, le réseau des fleuves, des rivières et des canaux d’une contrée quelconque, en y ajoutant, à volonté, les côtes et les frontières.
On recouvre le dessin d’une feuille de carton opaque, de manière à ne pas conserver le souvenir du plan du labyrinthe; cette feuille de carton est percée d’un trou que nous appellerons oculaire, et qui permet seulement d’apercevoir une petite fraction du réseau. On déplace le carton ou l’écran, de telle sorte {47} que l’oculaire se trouve placé sur un carrefour A. Il s’agit ensuite de faire parcourir deux fois à l’oculaire toutes les lignes du réseau, d’une manière continue, et de revenir ensuite au point de départ A. Pour conserver le souvenir du passage de l’oculaire sur chacun des chemins qu’il parcourt, on trace sur chaque ligne suivie un petit trait transversal, à l’entrée et à la sortie des carrefours. Par conséquent, les deux extrémités de chaque chemin devront, après les pérégrinations du voyage, avoir été marquées deux fois, mais non davantage.
Dans un labyrinthe effectif, ou dans une galerie de mines, le promeneur égaré déposera une marque, un caillou, à l’entrée et à la sortie de chaque carrefour, dans l’allée qu’il vient de quitter et dans celle qu’il vient de prendre.
Parmi les diverses solutions de ce curieux problème de la Géométrie de situation, dont nous venons de donner l’énoncé, nous choisirons, comme la plus simple et la plus élégante, celle qui nous a été gracieusement communiquée par M. Trémaux, ancien élève de l’École Polytechnique, ingénieur des télégraphes; mais nous en avons modifié légèrement la démonstration.
Première règle. – En partant du carrefour initial, on suit une voie quelconque, jusqu’à ce que l’on arrive à une impasse ou à un nouveau carrefour: 1° si le chemin qu’on a suivi aboutit à une impasse, on revient sur ses pas, et l’on peut alors considérer le chemin parcouru comme supprimé, puisqu’il a été traversé deux fois; 2° si le chemin aboutit à un carrefour, on prend {48} une voie quelconque [10], au hasard, en ayant soin de marquer d’un trait transversal la voie d’arrivée dans le sens de la flèche f, et la voie de départ dans le sens de la flèche g (fig. 9). Dans cette figure et dans les trois suivantes, nous avons distingué les anciennes marques des nouvelles, en surmontant celles-ci d’une petite croix.
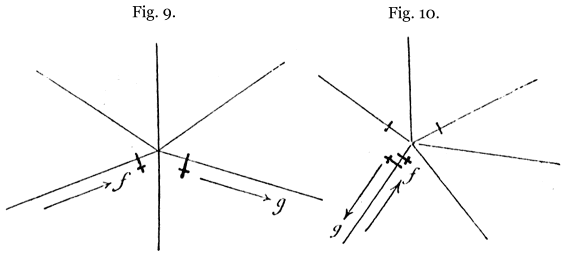
On continue l’application de la première règle, chaque fois que l’on arrive à un carrefour inexploré; au bout d’un certain parcours, on arrivera nécessairement à un carrefour déjà exploré; mais cette situation peut se présenter de deux manières différentes, selon que le chemin d’arrivée a déjà été suivi une première fois ou ne contient encore aucune trace de passage. Alors on applique l’une des deux règles suivantes:
Deuxième règle. – En arrivant à un carrefour déjà exploré, par une voie nouvelle, on doit rétrograder, en marquant par deux traits l’arrivée au carrefour et le départ, ainsi qu’on le voit dans la fig. 10.
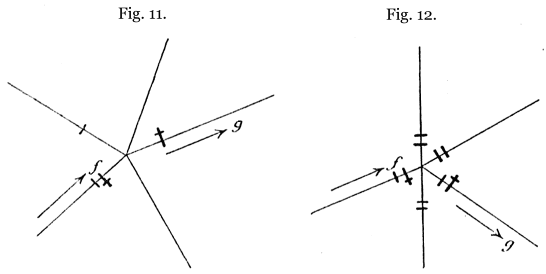
Troisième règle. – Lorsqu’on arrive à un carrefour déjà exploré par une voie antérieurement suivie, on prendra d’abord {49} une voie qui n’aura pas été parcourue, s’il en existe, ou, à son défaut, une voie qui n’aura été parcourue qu’une seule fois; ces deux cas sont représentés dans les fig. 11 et 12.
Démonstration. – En exécutant rigoureusement l’application des règles précédentes, on parcourra nécessairement deux fois toutes les lignes du réseau. D’abord on fera les remarques suivantes:
I. Au départ du carrefour A, on y introduit une seule marque initiale.
II. Le passage à travers un carrefour, par l’emploi de l’une des trois règles, ajoute deux marques aux lignes qui aboutissent à ce carrefour.
III. A un moment quelconque de l’exploration du labyrinthe, avant l’arrivée au carrefour ou après le départ du carrefour, le carrefour initial contient un nombre impair de marques, et tout autre carrefour en contient un nombre pair.
IV. A un moment quelconque de l’exploration, avant ou après le passage au carrefour, le carrefour initial ne peut avoir {50} qu’un seul chemin, marqué une seule fois; tout autre carrefour exploré ne peut avoir que deux chemins marqués une seule fois.
V. Après l’exploration complète, tous les carrefours doivent être couverts de deux marques sur chaque chemin; c’est la condition imposée par l’énoncé.
Cela posé, il est facile de voir que, lorsque le voyageur arrive dans un carrefour M différent du carrefour initial A, il ne peut être arrêté dans sa course par les difficultés du problème. En effet, on ne peut arriver à ce carrefour M que par une voie nouvelle, ou par une voie déjà parcourue une seule fois. Dans le premier cas, on applique la première ou la deuxième règle; dans le second cas, l’entrée au carrefour produit un nombre impair de marques; il reste donc, d’après la Remarque III, à défaut d’une voie nouvelle, une ligne qui n’a été traversée qu’une seule fois.
Ainsi, il ne peut y avoir d’arrêt qu’en revenant au carrefour initial A. Soit ZA le chemin qui conduit au repos forcé, en venant du carrefour Z; ce chemin est nécessairement un chemin parcouru une première fois, car sans cela on pourrait continuer le voyage. Puisque le chemin ZA a déjà été traversé, il n’existe dans le carrefour Z aucune voie n’ayant point encore été traversée, car sans cela on aurait oublié d’appliquer le premier cas de la troisième règle; d’ailleurs, il y avait en dehors de ZA une voie, et une seule, YZ, parcourue une seule fois, d’après la Remarque IV. Par conséquent, au moment de l’arrêt en A, toutes les routes du carrefour Z ont été traversées deux fois; on démontrera, de même, que toutes les voies du carrefour précédent Y l’ont été deux fois, et ainsi des autres carrefours. C’est ce qu’il fallait démontrer.
{51} Rémarque. – On peut remplacer la deuxième règle par la suivante, quand il ne s’agit pas d’un carrefour fermé. Si l’on arrive, par une voie nouvelle, à un carrefour déjà exploré, on peut prendre une nouvelle voie, à la condition d’affecter les deux marques du passage au carrefour d’indices correspondents a et a′; alors, si l’on retourne au carrefour par l’une de ces deux voies, on doit reprendre l’autre. Cela revient, pour ainsi dire, à placer un pont aa′ au-dessus du carrefour. Cette règle nous a été indiquée par M. Maurice, ancien élève de l’École Polytechnique.
Nous avons vu que, dans l’application de la seconde règle, on doit rétrograder quand on arrive, par une voie nouvelle, à un carrefour exploré. Supposons que l’on supprime, dans le réseau, un petit fragment du chemin qui aboutit à ce carrefour, et que l’on fasse la même opération à tous les endroits de recul; le réseau se transforme alors dans une autre figure géométrique que l’on désigne indistinctement sous le nom d’arbre, de ramification, d’arborescence; les chemins prennent le nom de branches ou de rameaux, et les carrefours le nom d’embranchements ou de nœuds. De pareilles configurations ont été étudiées par MM. Jordan, Sylvester, Cayley, Septimus Tebay, et tout récemment par M. le prince C. de Polignac (1).
(1) Jordan, Journal de Borchardt. – Sylvester, Educational Times. – Cayley, British Association Report, 1875. – De Polignac, Bulletin de la Société mathématique, t. VIII, p. 120.
On donne habituellement de l’arbre géométrique la définition {52} suivante: De chaque nœud on peut, en suivant les branches, parvenir à un nœud quelconque, mais par un seul chemin. Cette théorie a été considérablement simplifiée par M. de Polignac au moyen d’une remarque fondamentale. En effet, toute ramification peut être tracée au moyen d’un certain nombre de traits continus, sans répétition ni arrêt, c’est-à-dire en partant de l’extrémité d’une branche et en continuant jusqu’à ce que l’on arrive à l’extrémité d’une autre branche ou à une branche déjà parcourue. Observons que le trait doit traverser une ligne quoique déjà tracée, s’il peut continuer au delà, sans cheminer le long de cette ligne. Cela posé:
Remarque fondamentale.– De quelque manière que l’on trace une ramification sans répétition ni arrêt, le nombre des parcours sera toujours le même.
En effet, faisons une coupure à toutes les branches joignant deux nœuds, on décomposera la ramification en une série d’étoiles. On recomposera la ramification en rendant aux étoiles leurs rayons communs. Pour chaque étoile, prise séparément, la propriété fondamentale est évidente. Désignons par N1, N2, N3, …, Np, les nombres des traits relatifs à chaque étoile; par p le nombre des nœuds ou des étoiles. Si l’on réunit maintenant les deux premières étoiles, on perd un trait sur la somme des parcours relatifs à chaque étoile; réunissons la deuxième étoile à la troisième, nous perdons encore un trait; par suite, si l’on désigne par N le nombre des traits qui ont servi à tracer la ramification, on a
| N = N1 + N2 + N3 + … + Np − (p − 1) . |
Nous appellerons le nombre N la base de la ramification; on {53} peut exprimer les nombres N1, N2, …, et par suite le nombre N lui-même d’après l’ordre des nœuds, ou étoiles, c’est-à-dire par le nombre de branches ou de rayons qui y aboutissent. Le nœud le plus simple est le nœud ternaire ou d’ordre 3; soit, en général, mq l’ordre d’un nœud on a d’abord m au moins égal à trois; le nombre Nq des traits qui permettent de dessiner ce nœud est égal à la moitié de mq, si mq est pair, et à la moitié de mq + 1, lorsque mq est impair; c’est donc, dans tous les cas, le plus grand nombre entier contenu dans la fraction (mq + 1)/2.
Ce nombre est habituellement représenté par le symbole
| [ | mq + 1 | ] | ; |
| 2 |
par conséquent la formule précédente peut s’écrire
| N = | [ | m1 + 1 | ] | + | [ | m2 + 1 | ] | + … + | [ | mq + 1 | ] | − (p − 1) . |
| 2 | 2 | 2 |
On détermine ainsi la base de la ramification connaissant le nombre et l’ordre des nœuds.
Désignons par l le nombre des extrémités libres des branches, et supposons que la ramification n’ait que des nœuds d’ordre ternaire; on a alors, quel que soit le nombre des nœuds ternaires, la formule
| N = l − 1 . |
Cette formule est évidente pour une étoile à trois rayons; si l’on ajoute un nœud ternaire à l’extrémité libre d’une branche, on remplace celle-ci par deux autres, et l’on ajoute un trait; lorsque l’on forme un nœud ternaire par l’addition d’un rameau sur une branche, on ajoute un trait et une extrémité libre. Dans les deux {54} cas, les deux membres de la formule précédente augmentent d’une unité. Donc cette formule est générale.
Désignons en général par pk le nombre des nœuds d’ordre k; on a, pour deux nœuds séparés d’ordre quaternaire ( p′4 et p″4 étant l’unité),
| N′ = l′ − 1 − p′4 , N″ = l″ − 1 − p″4 . |
En réunissant deux nœuds quaternaires par une extrémité commune, le nombre total des traits diminue d’une unité, mais deux extrémités disparaissent; on a donc
| N + 1 = N′ + N″ , l′ + l″ = l + 2 , p′4 + p″4 = p4 ; |
par suite, on a pour la ramification des deux nœuds quaternaires
| N = l − 1 − p4 ; |
cette formule s’applique à une ramification formée d’un nombre quelconque de nœuds quaternaires. On démontrera de même que la base d’une ramification ne contenant que des nœuds de cinquième ordre en nombre p5 est donnée par la formule
| N = l − 1 − p5 . |
Plus généralement, lorsqu’une ramification ne contient que des nœuds d’ordre 2μ, on a
| N = l − 1 − (μ − 1)p2μ ; |
et lorsqu’elle ne contient que des nœuds d’ordre 2μ + 1, on a encore
| N = l − 1 − (μ − 1)p2μ + 1 . |
{55} Par suite, en réunissant deux ou plusieurs ramifications par deux extrémités libres, on obtient la formule générale
| N = l − 1 − (p4 + p5) − 2(p6 + p7) − 3(p8 + p9) − 4(p10 + p11) − … . |
Nous indiquerons dans la Note III placée à la fin du volume les divers rapprochements que l’on peut établir entre la théorie des arbres et le jeu des ponts et des îles.