Maximum discrepancy between straight line and geodesic on OS maps
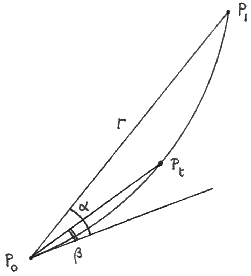
The diagram shows points P0, P1 on an Ordnance Survey map. The straight line P0P1 is as drawn by a ley-hunter; the curve P0P1 is the projection of the true geodesic. Required, the maximum distance between them.
Work in units of 100 km as in the 1977 notes. Let Pi have National Grid coordinates (Ei, Ni) and let Di = Ei − 4. Let P0P1 = r so that
| r 2 = (D0 − D1)2 + (N0 − N1)2. | (1) |
Let Pt be the point on the curve P0P1 whose distance from P0 is t times the length (0 ≤ t ≤ 1). Let Grid Az − Plane Az for P0P1 and P0Pt be α and β respectively. Then (to a first approximation) Pt is offline by
| t r ǀ α − β ǀ . | (2) |
From the 1977 notes we have
| α = k (2D0 + D1) (N1 − N0) | (3) |
| β = k (2D0 + Dt) (Nt − N0) |
where
| k = 0.002345(π/180) | (4) |
and to a first approximation
| (Dt, Nt) = (1 − t) (D0, N0) + t (D1, N1). | (5) |
Hence Pt is offline by
| k r ǀ N0 − N1 ǀ ǀ f (t) ǀ | (6) |
where
| f (t) = (D0 − D1) t 3 − 3D0 t 2 + (2D0 + D1) t. | (7) |
The turning points of f (t) are at
| t = (D0 − D1)−1(D0 ± Q1/2) | (8) |
where
| Q = (D02 + D0D1 + D12) / 3. | (0) |
At the turning points
| ǀ f (t) ǀ = (D0 − D1)−2 ǀ D0D1(D0 + D1) ± 2Q3/2 ǀ . | (10) |
When both turning points satisfy 0 ≤ t ≤ 1 we want to choose the one that makes the terms inside the modulus have the same sign. Suppose w.l.o.g. that D0 D1; then there are four cases.
| Case 1. | D0 < D1 < 0; upper sign forced; opposite signs. |
| Case 2. | 0 < D0 < D1; lower sign forced; opposite signs. |
| Case 3. | D0 < 0 < D1 with D0 + D1 ≤ 0; upper sign may be chosen; same sign. |
| Case 3. | D0 < 0 < D1 with D0 + D1 ≥ 0; lower sign may be chosen; same sign. |
The following formula therefore applies to all four cases:
| ǀ f (t) ǀmax = (D0 − D1)−2 │ D0D1 ǀ D0 + D1 ǀ − 2Q3/2 │ . | (11) |
Now let A be the azimuth of P0P1 and define
| q = ǀ (D0 + D1)cosec A ǀ. | (12) |
Then
| ǀ D0 − D1 ǀ = r ǀ sin A ǀ, ǀ N0 − N1 ǀ = r ǀ cos A ǀ | (13) |
so from (6) and (11) we find that the maximum discrepancy on the ground caused by replacing the geodesic by a straight line on the map is
| 0.5116 ǀ sin2A ǀ ǀ q(q2 − r2) − (q2 + r2/3)3/2 ǀ metres | (14) |
where the constant is 100000k / 8.
Example
The so-called St Michael’s line from St Michael’s Mount to Bury St Edmunds Cathedral. The endpoints are given by
| E0 = 1.5146, N0 = 0.2987, so D0 = −2.4854, |
| E1 = 5.8559, N1 = 2.6414, so D1 = +1.8559. |
Hence
| A = 61.647°, q = 0.7153, r 2 = 24.3551 |
and from (14) the maximum discrepancy is 18.1 metres.
Michael Behrend
2 December 1985