Generalization of strip formula to discs of different sizes

These notes, dated 30 June 1985, provide a generalization of the strip method for estimating the number of chance alignments in a random set of sites.  The sites are supposed to be discs, and a set of sites is considered to be aligned if a straight line can be drawn that intersects all the discs.  The discs are now allowed to be of different sizes, whereas in the strip formula they are required to be all the same size. 

The clarification at the end was added at the time, in response to a reader who complained that the proof was “very hard going”.  The note on practical calculation was added in January 2014.  MB

The area (e.g. Ordnance Survey map) in which the sites lie is assumed to be a bounded convex subset K of E².  The sites are S₁,…,S_n where each S_i is a closed connected subset of K whose width in any direction is small compared with the dimensions of K.  A set of r≥3 sites is considered to form an alinement iff there exists a straight line L meeting each site in the set.  Note that L meets S_i iff L meets the convex hull S_i of S_i.  We suppose that for each i the position of S_i in K and the orientation of S_i in (0,2π) have uniform distributions, and that the 2n distributions are independent.  We derive a formula for the expected number of r-site alinements among the n sites, having length less than a given length q. 

The mean width d_i of S_i is defined as follows.  Given a line L of azimuth θ let w_i(θ) be the width of the projection of S_i onto L.  Then

di= 1 ∫ 2π wi(θ)dθ. 2π 0

(1)

Equivalently, d_i is defined by the fact that πd_i is the perimeter of S_i (easy proof ).  For each i, let P_i be a point inside, and fixed relatively to, S_i (say the centroid of S_i). 

We first investigate the probability that S₁,…,S_r form an r-site alinement with end sites S₁ and S₂.  The required formula will then follow by a simple combinatorial argument. 

First fix P₁,P₂ so that P₁P₂=t<q.  We may assume that t is large compared with the dimensions of the S_i.  Take (x,y)-axes with origin at P₁ so that P₂ is at (t,0).  Let P_i be at (x_i,y_i).  Next fix the orientations of the S_i, and let the maximum and minimum y-coordinates of points in S_i then be y_i+b_i±c_i.  For 3≤i≤r let x_i be restricted to some small interval in (0,t); say

tui<xi<t(ui+δui), 0<ui<1.

(2)

Let L be a movable straight line meeting S₁ and S₂; say L passes through (0,z₁) and (t,z₂) where

|zi−bi|<ci (i=1,2).

(3)

For given (z₁,z₂) the line L meets the other sites iff

|(1−ui)z1+uiz2−yi−bi|≤ci (3≤i≤r).

(4)

Let C(z₁,z₂) in E^r−2 be the cuboid of all ( y₃,…,y_r) such that (4) holds.  We want to find the content of the (r−2)-dimensional solid U given by

U= ∪ {C(z1,z2)│(3)holds}.

(5)

Let W in E^r be the cuboid

W={(z1,…,zr)│|zi−bi|≤ci}

and let V in E^r−1 be the image of W under the linear map

g:(z1,…,zr)→(z1−z2,y3,…,yr),
yi=(1−ui)z1+uiz2−zi.	(6)

Let ƒ be the projection from E^r−1 to E^r−2 given by

ƒ:( y0,y3,…,yr)→( y3,…,yr)

(7)

so that U=ƒ(V).  Since V is convex, each point in the interior of U is the image of exactly 2 points on the boundary of V.  Hence

U= 1 ∑ |ƒ(X)| 2

(8)

summing over all faces X of V.  Clearly each face X of V is the image g(Y ) of some face Y of W (not conversely).  Fix i and j with 1≤i<j≤r and consider the set of 4 faces Y given by

Y:zi=bi±ci, zj=bj±cj.

(9)

Since coordinates 1 and 2 are distinguished there are 4 cases. 

Case 1: i>2 and j>2. 

Let h be the linear function on E^r−1 given by

h( y0,y3,…,yr)=(ui−uj)y0+yi−yj .

(10)

Then by (6) and (10)

h(g(z1,…,zr))=−zi+zj

(11)

so that h is constant on g(Y ).  The signs on the RHS of (11) are opposite, hence g(Y ) is a face of V iff the signs in (9) are taken opposite.  If X=g(Y ) is such a face then we easily calculate

|ƒ(X)|=|ui−uj| ∏   (2ck). k≠i,j

(12)

Case 2: i=2,j>2.  The same argument with

h( y0,y3,…,yr)=(1−uj)y0−yj

(13)

leads to 2 faces X of V such that

|ƒ(X)|=|1−uj| ∏   (2ck). k≠2,j

(14)

Case 3: i=1,j>2. 

h( y0,y3,…,yr)=ujy0+yj

(15)

|ƒ(X)|=|uj| ∏   (2ck). k≠1,j

(16)

Case 4: i=1,j=2. 

h( y0,y3,…,yr)=y0

(17)

|ƒ(X)|= ∏   (2ck). k≠1,2

(18)

For convenience define

u1=0, u2=1.

(19)

Then substituting into (8) from (12), (14), (16) and (18) (recall that each describes 2 faces X) we get

|U|= ∑   |ui−uj|Cij 1≤i<j≤r

(20)

where

Cij= ∏   (2ck). k≠i,j

(21)

So if now P₃,…,P_r vary freely, the probability that S₁,…,S_r form an alinement with end sites S₁,S₂ is

|K|2−rtr−2 ∫ 1 … ∫ 1 |U|du3…dur 0 0
=|K|2−rtr−2 ( C12+ 1 ∑   C1j+ 1 ∑   C2j+  1 ∑   Cij ) . 2 j>2 2 j>2 2 i,j>2	(22)

Since the orientations of the S_i are independent and uniform, we can now allow them to vary and replace each in (22) by its mean value

∏   dk . k≠i,j

Now allow the end sites to be any pair of S₁,…,S_r.  To sum all the terms such as (22) note that the sum of the coefficients of the C_ij in (22) is

1+  1 (r−2)+  1 (r−2)+  1 (r−2)(r−3)=  1 r(r+1). 2 2 6 6

so that the probability that S₁,…,S_r are alined is

|K|2−rtr−2⋅ 1 r(r+1) ∑   ∏     dk . 6 i<j k≠i,j

(23)

If any set of r sites can be chosen, we get ⁿC_r expressions like (23) in which each product of d’s appears ^n−r+2C₂ times.  Finally, let the distance t=P₁P₂ between the independently and uniformly distributed points P₁,P₂ of K have p.d.f. p(t).  Then the expected number of r-site alinements of length less than q among the n sites S₁,…,S_n is given by

1 (n−r+2)(n−r+1)r(r+1) ∑   di1…dir−2|K|2−r ∫ q p(t)tr−2dt. 12 i1<…<ir−2 0

If the orientations of the S_i are non-uniform (but still independent) one could try modifying the above argument, using the joint p.d.f. of t,θ where θ is the azimuth of P₁P₂.  Note that if K is a disc then the formula applies even for non-uniformly distributed orientations.  If K is a square the discrepancy is likely to be small. 

(March 2013) We check that the above formula reduces to the strip formula when the alinements have unlimited length (q=∞) and the discs are all the same size (d_i=2c for each i).  In this case

∑   di1…dir−2=nCr−2(2c)r−2,  ∫ ∞ p(t)tr−2dt=Mr−2 , i1<…<ir−2 0

so that with the notation A=|K| the result is seen to be the same as for the strip formula. 

Clarification

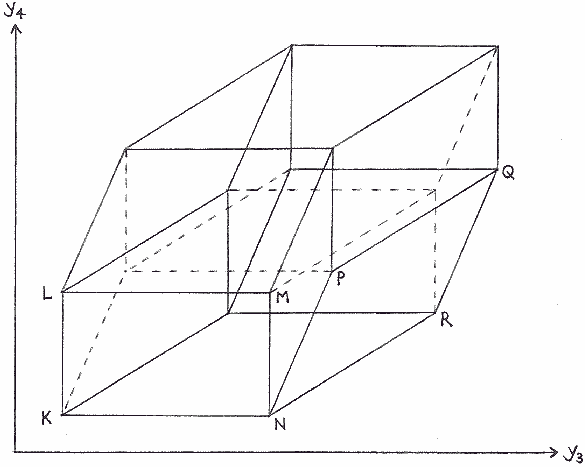
The above diagram, drawn for the case of 4-point alinements, may clarify the idea behind the proof. 

The cuboid C(z₁,z₂) is a movable rectangle, of which KLMN is a particular position.  As z₁,z₂ vary, so the lower right corner of the rectangle moves over the parallelogram NPQR.  Thus U, the union of the rectangles, is the octagon formed by the outer edges of the figure. 

By drawing in the solid lines inside U we see that U is the projection of a 3-dimensional solid V with 12 parallelogram faces.  The projections of the faces of V cover U exactly twice. 

By drawing in the dotted lines (which represent lines inside V) we see that V in turn is the projection of a 4-dimensional cuboid W.  Each face of V is the projection of a 2-dimensional face of W.  The 2-dimensional faces of W fall into groups of 4, of which 2 project into faces of V, while 2 project into the interior of V and are excluded from the calculation. 

Practical calculation

Recall that we are given the diameters d₁,…,d_n of the n discs.  For r-point alinements, r=3,4,5,…, define m=r−2.  The formula above requires the calculation of S_m, the sum of all products of m diameters with distinct indices.  Formally

Sm= ∑   di1…dim. 1≤i1<…<im≤n

In principle this could be done by simply working through all m-element subsets of 1,…,n and adding the products.  In practice this approach is likely to take far too much computer time.  A better method is as follows. 

For m=1,2,3,… define

Pm=d1m+d2m+⋯+dnm.

It is not difficult to show that

S1=P1 2S2=P1S1−P2 3S3=P1S2−P2S1+P3 4S4=P1S3−P2S2+P3S1−P4 5S5=P1S4−P2S3+P3S2−P4S1+P5

and so on.  These formulae allow S₁,S₂,S₃,… to be calculated in succession.