
Translated from “Le jeu des ponts et des îles”,
E. Lucas, Récréations mathématiques, vol. I (2nd edn, Paris, 1882), ch. 2, pp. 21–38.
Lucas’s four-volume work, of which two chapters are republished on this website, is one of the classic books on recreational mathematics. In this chapter Lucas provides a translation of Euler’s paper on the Königsberg bridges, and adds some notes on similar unicursal problems.
{21}
Among the various works of mathematicians on that branch of the science of area called geometry of position, we meet right at the start a famous paper by Euler, known as the Königsberg bridges problem; we will give, following the Nouvelles Annales de Mathématiques [4], a commentary on this work, which appeared in Latin in the Mémoires de l’Académie des Sciences de Berlin for 1759 [5], and which is entitled “Solutio problematis ad Geometriam situs pertinensis” .
Here (pages 21–33) Lucas inserts a French translation of Euler’s paper. The French is not here translated into English, since an English translation direct from the Latin can be found on this website.
{33}
Here Euler’s paper ends. This famous geometer has only dealt with (so to speak) the question of impossibility. In Note II, at the end of this volume, can be found the theory of possibility, which must be considered as a sequel to the paper just given.
We shall now apply the rules proved in Euler’s paper to the following problem: Is it possible to cross all the bridges of Paris in succession without crossing any of them twice?
We shall include in this problem only the bridges over the Seine, ignoring canals. In the its course through Paris, the river meets with only three islands, namely: the Île Saint-Louis, the Cité and the Île des Cygnes. Consequently we have to count five different regions: the two banks and the three islands.
{33} But, among these five regions, the Île des Cygnes and the Cité are even regions (i.e. regions with an even number of bridges into them); to the first lead the two parts of the Pont de Grenelle; to the Cité there lead ten bridges, namely: (1) on the south, the Pont de L’Archevêché, the Pont au Double, the Petit-Pont, the Pont Saint-Michel and the southern part of the Pont-Neuf; (2) on the north, the Point Saint-Louis, the Pont d’Arcole, the Pont Notre-Dame, the Pont au Change and the northern part of the Pont-Neuf. The Île Saint-Louis is an odd region to which lead seven bridges: to the south, the southern part of the Pont Sully, the Pont de la Tournelle and the Pont Saint-Louis; to the north, the northern part of the Pont Sully, the Pont Marie and the Pont Louis-Philippe; but we must add the Estacade, a wooden bridge leading to the right bank. As for the two banks, there is no need to know the number of bridges; it is easy to see that one of them is an odd region and the other an even region. For it was shown in Euler’s §17 that the number of odd regions is always even; now out of these five regions we have so far two even and one odd; it then follows that one or other of the banks must be the starting-point of an odd number of bridges.
Furthermore, since there are only two odd regions, the problem proposed is always possible. In other words, a traveller can so arrange his journey that he is able to pass once, and once only, over all the bridges that lead to the Cité and the Île Saint-Louis and over any number of bridges directly joining the two banks of the Seine. But the walker is always forced to take the Île Saint-Louis as a starting or finishing point.
We shall also remark that if the Estacade is ignored, the problem becomes a very simple one.
{35}
The problem is sometimes set of drawing, in a single movement and without doubling any line, the figure formed by the four sides of a rectangle and its two diagonals. This problem is similar to that of the Königsberg bridges; let A, B, C, D be the vertices of the rectangle, E the intersection of the diagonals. The five points can be treated as the centres of five areas; four of them, A, B, C, D, are odd; thus the problem is impossible. However, one could draw this figure by doubling all the lines.
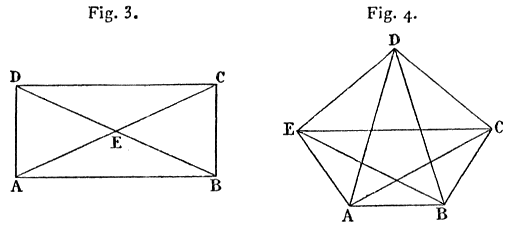
These considerations apply to the drawing in a single movement of all geometrical figures made up of lines, be they straight or curved, in a plane or in space. Thus it can very easily be shown that one can draw in a single movement the figure formed by the sides and all the diagonals of a convex polygon with an odd number of sides, and that the problem is impossible for even polygons, such as the square or the hexagon. In the same way, one can draw in a single movement the set of edges of {36} a regular octahedron, whereas it cannot be done for the other four convex regular polyhedra.
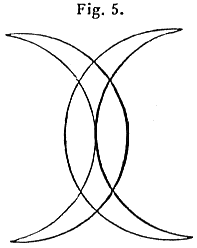
I dare say Muhammed drew in one stroke, with the point of his scimitar, his signature of two crescents back to back, as shown in fig. 5. Indeed, this figure contains only points of even order, and can be drawn in a single continuous movement.
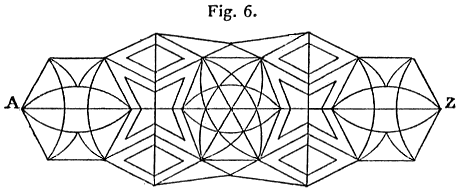
Fig. 6 contains only two odd points A and Z; consequently, it can be drawn in a single continuous movement going from A to Z or conversely. You can make a game by drawing an enlargement of this figure on a sheet of cardboard; small counters are placed on the middle of all the lines joining two neighbouring points; {37} it is then a question of finding what course to follow in order to remove all the counters in succession. This figure is taken from a booklet entitled Vorstudien zur Topologie, by Johann Benedict Listing; this curious work was kindly communicated to me by M. Moritz Cantor, a professor at Heidelberg University.
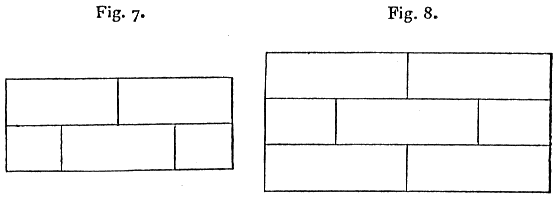
Fig. 7 contains eight odd points and cannot be drawn in fewer than four continuous movements; this theorem was stated by Clausen, in issue 494 of the Astronomische Nachrichten. Fig. 8 represents a piece of brick wall; it contains twelve odd points, and cannot be drawn in fewer than six continuous movements.
Similarly, the figure that represents the ordinary chess board of sixty-four squares contains twenty-eight odd points, and cannot be drawn in fewer than fourteen movements; the draughts board of one hundred squares [6] requires a sequence of eighteen continuous movements.
If the sides of a triangle are divided into n equal parts, and if corresponding points are joined by lines parallel to the sides, we obtain a figure that contains only {38} points of even order, and can be drawn in a single movement, etc.
Another problem that reduces to the Königsberg bridges is that of the journey of a smuggler who intends to cross all the respective borders of the various countries of a continent, and to cross them only once. It is obvious that the various countries and their borders correspond exactly to the regions and the branches of the river, if a single bridge were thrown across each of them, for each common border has two countries. Thus, since Sweden, Spain and Denmark have an odd number of borders, [7] it is impossible to cross, only once only, all the borders of the various countries of Europe.
It remains to consider the corresponding geometrical problem for plane and three-dimensional figures. Thus, by a continuous movement over the surface, it is possible to cross all the edges of the cube once only, but not the edges of the other convex regular polygons.