Dénes König, “The labyrinth problem”

Chapter Three.

The Labyrinth Problem.

§ 1. Statement of the problem. Wiener’s solution.

Theorem II 5 is closely related to the labyrinth problem¹), which will be treated in this chapter. Since the width of the alleys need not be considered, a labyrinth can be identified with a graph, more precisely a finite and connected graph; the vertices of this graph correspond in the labyrinth to the branch points and the endpoints of the blind alleys. So for instance the labyrinth of 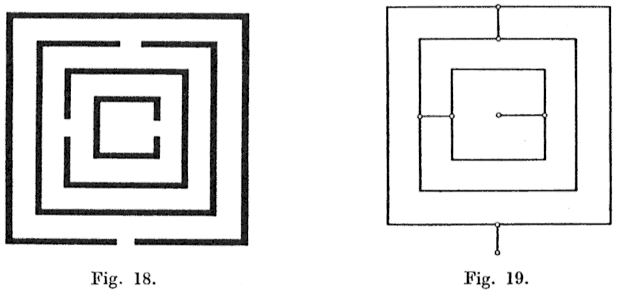Fig. 18 corresponds to the graph of Fig. 19 (or also the graph of Fig. 20). It is now required to give a method for reaching a specified point, which is usually treated as the centre of the labyrinth. Since it is entirely arbitrary which point is treated as the centre, the problem is only to be solved by specifying a way to reach every point of the labyrinth. If the plan of the whole {36} labyrinth is known, there is of course, since there are only finitely many possibilities, no difficulty. We do not however wish to assume that we know the plan of the labyrinth. Instead, all that will be assumed is that, if while walking in the labyrinth one reaches any branch point X (or the endpoint X of a blind alley), the labyrinth (the graph) is known “in the neighbourhood of X ”, i.e. the alleys (edges) ending at X are known, as are also certain properties of the path already covered, insofar as these relate to the point X just reached.

¹) Almost all works on recreational mathematics give some attention to labyrinths. Apart from the already-mentioned passages in the books by Lucas, Rouse Ball, and Ahrens, we may also mention: H. E. Dudeney, Amusements in Mathematics, London 1917, where many labyrinths can be found (pp. 127–137).

We will first assume that if during the journey one arrives at a vertex P, it is known for every edge ending at P whether it has already been traversed; besides this we assume that (like Theseus with the aid of Ariadne’s thread) one can at any moment retrace in the opposite direction the whole of the path already covered (with the same repetitions). Under these assumptions the problem was solved by Wiener, [1]¹) who was the first ever to treat the age-old problem of the labyrinth as a mathematical one. – Wiener’s instructions (in a somewhat specialized form) run as follows:

¹) Here we are concerned with the second part of this note. The first part (where Wiener tacitly restricts himself to plane labyrinths) has no real mathematical content, since the problem solved there, that of specifying a method for finding one’s way back to the starting-point, has a trivial solution: stay where you are.

Starting at an (arbitrary) vertex A, choose entirely at random the edges AB, BC, CD, … until you arrive at an endpoint (dead end) Q of the graph or at a vertex Q that has already been visited. Having arrived at Q, retreat and follow in reverse the route already covered, until you first arrive at a vertex R at which there is an edge that has not yet been traversed. Having arrived at this R, deviate and follow any as yet untraversed edge RS, then continue the journey over untraversed edges in an arbitrary way, until you arrive at an endpoint or a vertex that has already been visited; here retreat, etc.

We prove that the sequence of edges ABC…Q…RS… (i) leads back to A and (ii) then contains every edge of the graph.

If there is no deviation at all, one will naturally arrive back at A. But if there is a deviation, then since at every deviation a new edge is added [to those already covered] and the graph has only finitely many edges, there must {37} be a final deviation. Since the number of vertices is also finite, one must after this deviation reach an endpoint or an already-visited vertex Z. According to our instructions one must then, since no further deviation is possible, traverse this whole sequence of edges F=AB…Z in the reverse direction, so that one does indeed arrive back at A.

That every edge of the original graph G has been traversed, is proved as follows. Let us assume that this is not the case: then the untraversed edges form a proper subgraph G″ of G, while the traversed edges form the (connected) subgraph G′ of G. G′ and G″ have no common edge; they have however at least one common vertex P, for otherwise G=G′+G″ (Theorem I 24) would not be connected. Since P belongs to G′, P is a vertex of the edge sequence F=AB…Z. Since P also belongs to G″, there is an untraversed edge ending in P. During the above-mentioned traversal of G in the direction of A we must therefore deviate at P. And this contradicts the fact that the last deviation has already taken place.

§ 2. Trémaux’s solution.

The above-described method of Wiener cannot be called economical, since in general the edges have to be walked through a great many times. This is the more noticeable in that – by Theorem  II 5 – there is a journey through all the edges of the graph in which no edge is traversed more than twice. We shall show that such a solution can still be found under the assumption, not that the entire graph is known beforehand, but only that certain local properties are known at any moment after starting the journey.

We will, however, no longer suppose that the route already covered can always be retraced in the reverse direction, but instead of this supposition of Wiener’s we make the (partly stronger and partly weaker) assumption that, on arrival during the journey at any vertex P, it is known for every edge ending at P whether it has already been walked, and if so how many times (the directions in which the edges have been walked are not assumed to be known here). Under this assumption, the labyrinth problem has been solved in an elegant way by Trémaux¹. His procedure is as follows:

¹ See Lucas [1, vol. I, pp. 47–51]. {38} If, after starting at an arbitrary vertex A₁, you arrive via an edge PQ at a vertex Q which is not an endpoint (dead end) of the graph and which you are visiting for the first time, then continue the journey with any other edge QR. But if Q has either been visited before or is an endpoint and PQ has just been walked for the first time, then retreat, i.e. continue the journey with the same edge PQ (in the reverse direction QP). If both Q and PQ have been visited before, proceed along any unused edge QR or, if no such edge is available, along an edge QR that has been used only once.

If these rules are followed, then every edge is travesred at most twice; since the number of edges is finite the journey must therefore come to an end, i.e. you must sometime arrive at a vertex K such that all edges ending at K have already been traversed twice. Moreover, we must have K=A₁, for otherwise we should have (for the endpoint K of an open sequence of edges) a contradiction to Theorem I 2. We shall now prove Trémaux’s theorem, which states that when the procedure is broken off on some¹ arrival at A₁ every edge has been traversed twice, that is, once in each direction. We wish to set out our rather complicated proof in full detail, the more so since we are not aware of any complete proof of Trémaux’s theorem in the literature.²

¹The journey must not broken off merely because you have arrived back at A₁ for the first time.

²Trémaux did not, it seems, publish his proof. The proof by Lucas [1, vol. I, pp. 47–51] is – so he says – a slight modification of Trémaux’s. This proof by Lucas is not complete, for firstly the case that the edges denoted there by ZA and ZY are identical (a case that can actually happen) is left out of consideration, and secondly an essential statement at the end of the proof is dealt with by the brief remark “on demontrera de même”. – In Ahrens [2, vol. II, pp. 192–194] both these critical points are treated in more detail, but even his proof contains an important omission, to which we shall shortly return (see following footnote). – It may be remarked here that neither Lucas nor Ahrens mentions the corollary that the edges are walked twice in opposite directions.

Let

A₁A₂,A₂A₃,…,A_ρ−1A_ρ,A_ρA_ρ+1,…,A_nA₁,(1)

in that order, be the edges that are covered in a regular (i.e. conforming to Trémaux’s rules) journey on a finite connected graph G. We first prove {39} that there must be in (1) an edge such that immediately after walking it the same edge is walked again (in the opposite direction), i.e. that you must retreat at least once. For let A_μ be the first member of the sequence A₁,A₂,A₃,… that has been visited before, say as A_ν (ν<μ). Two cases are now possible. (α) The edge A_μ−1A_μ has not been walked before; then, since A_μ has already been visited as A_ν, you must retreat, i.e. A_μ−1A_μ has the required property. (β) A_μ−1A_μ has been walked before, i.e. for some ρ<μ we must have A_μ−1A_μ=A_ρ−1A_ρ; but now A_μ−1 has not been visited before, and can thus because of ρ−1<μ−1 not be = A_ρ−1, whence A_μ−1=A_ρ; but, since for ρ<μ−1 we certainly have A_μ−1≠A_ρ, this can happen only in the case ρ=μ−1. Substituting this value of ρ [into the above], we obtain A_μ−1A_μ=A_μ−2A_μ−1, whence now A_μ−2A_μ−1 has the required property. (It can easily be shown that case (β) occurs if and only if A_μ−1 is an endpoint of G.)

Let therefore A_ρA_ρ+1 be an edge that is identical with the immediately preceding edge A_ρ−1A_ρ; thus A_ρ+1=A_ρ−1. If this edge A_ρA_ρ+1 (=A_ρ−1A_ρ) is removed from G, then the remaining edges form a subgraph G′ of G. We prove that the graph G′ is also connected. If A_ρ is an endpoint of G, this follows from Theorem I 14. If A_ρ is not an endpoint, then the retreat at A_ρ can be regular only if A_ρ has already been visited, and then some subsequence of the sequence (1) yields an open sequence of edges, not containing the edge A_ρ−1A_ρ, and joining A_ρ−1 to A_ρ. According to Theorem I 3 there then exists also in G a route not containing the edge A_ρ−1A_ρ and joining these two points. But then Theorem I 13 implies that G′ is indeed connected.

If in (1) A_ρ−1A_ρ and A_ρA_ρ+1 are deleted, there results likewise, since A_ρ−1=A_ρ+1, a sequence of edges:

A₁A₂,A₂A₃,…,A_ρ−2A_ρ−1,A_ρ+1A_ρ+2,…,A_μA₁.(2)

This represents a journey on G′, since A_ρ−1A_ρ (like every edge in general) can occur at most twice in (1), so that A_ρ−1A_ρ is not contained in (2). We prove that (2) gives a regular journey on G′, i.e. that if you arrive via any edge A_σ−1A_σ (where σ is distinct from both ρ and ρ+1) at A_σ, then by choosing the edge that immediately follows A_σ−1A_σ according to (2) you conform to Trémaux’s rules.¹

¹ In the above-mentioned proof by Ahrens of Trémaux’s theorem, this theorem, without being proved or formally stated, is implicitly used (on p. 193 and on p. 194) in an essential way.

{40} This is clear, if A_σ is distinct from both A_ρ and A_ρ+1 (=A_ρ−1), and again if σ<ρ−1, for in this case Trémaux’s rules permit the same possibilities for G′ as for G. Since σ=ρ and σ=ρ+1 are excluded, only the following three cases need to be dealt with: (α) σ=ρ−1; (β) σ>ρ+1 and A_σ=A_ρ; (γ) σ>ρ+1 and A_σ=A_ρ−1 (=A_ρ+1).

(α) We must show that in the transition from A_σ−1A_σ=A_ρ−2A_ρ−1 to A_ρ+1A_ρ+2 the rules are not broken. First (Fig. 21) 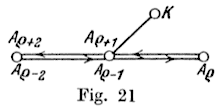suppose A_ρ−2A_ρ−1=A_ρ+2A_ρ+1 (so that A_ρ−2=A_ρ+2). Then a transition to the identical edge (retreat) is certainly regular in G′, if A_ρ−1 is an endpoint of G′ or has already been visited. And one of the two is certainly the case, for otherwise there would have to be a third and untraversed edge A_ρ+1K ending at A_ρ+1, and then during the journey on G you would have had to choose after A_ρA_ρ+1 not the edge A_ρ+1A_ρ+2, which has already been walked, but rather this edge A_ρ+1K. – Secondly suppose A_ρ+1A_ρ+2≠A_ρ−2A_ρ−1 (Fig. 22). 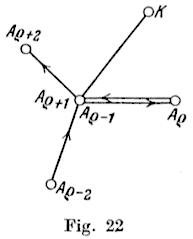After walking A_ρ−2A_ρ−1 in G′ you must not retreat, since A_ρ−1 is not an endpoint of G′ and since you would otherwise have had to retreat in the journey on G, so that A_ρ−2A_ρ−1 could not have been continued by A_ρ−1A_ρ. By passing from A_ρ−2A_ρ−1 to A_ρ+2A_ρ+1 in G′ we should therefore have broken the rules only if A_ρ+1A_ρ+2 had already been visited and a third edge A_ρ+1K had not been walked at all. But then in the journey on G A_ρA_ρ+1 would have had to be followed not by A_ρ+1A_ρ+2 but by A_ρ+1K.

(β) We prove that the rules are followed if during the journey on G′ the edge A_σ−1A_σ=A_σ−1A_ρ is allowed to be followed by the edge A_σA_σ+1=A_ρA_σ+1, provided that σ>ρ+1, so that the double traverse of A_ρ−1A_ρ has already taken place. Since A_ρ is not an endpoint of G (for there are at least two edges ending at A_ρ, namely A_ρ−1A_ρ and A_σ−1A_ρ), A_ρ must already have been traversed once, since otherwise this double traverse could not be regular. Thus if firstly A_σ−1A_ρ=A_σ+1A_ρ and thus A_σ−1=A_σ+1, then this retreat is also regular on G′. But if secondly A_σ−1A_ρ and A_ρA_σ+1 are distinct (Fig. 23), then A_σ−1A_ρ must have already been traversed for the second time (for otherwise you would have had to retreat); thus we cannot have broken the rules {41} 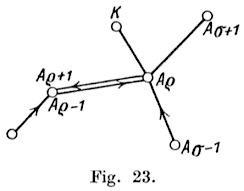unless there was a fourth and still untraversed edge A_ρK and A_ρA_σ+1 had already been traversed once; but then we should have already broken the rules by the same transition in the journey on G.

(γ) We show that the transition from A_σ−1A_ρ−1 to A_ρ−1A_σ+1 during the journey on G′ is regular, provided that this was the case for G and σ>ρ+1. Firstly suppose these two edges are identical, so that A_σ+1=A_σ−1. This retreat is regular, since A_ρ−1 has also been traversed during the journey on G′. If secondly A_σ−1A_ρ−1≠A_ρ−1A_σ+1 (Fig. 24), 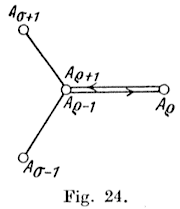then A_σ−1A_ρ−1 must already have been traversed once, and we can finish just as in the second case of (β).

This concludes the proof that (2) represents a regular journey on G′.

Now we can prove Trémaux’s theorem by complete induction on the number of edges, since the theorem holds for a graph with a single edge, as can be seen immediately. If during the journey on G given by (1), which satisfies Trémaux’s rules, you did not traverse every edge of G once in each direction, then of course not every edge of G′ would have been traversed once in each direction. But since we have proved that G′ is connected and that the journey (2) on G′ satisfies Trémaux’s rules, this is impossible; for we have assumed the truth of the theorem for the connected finite graph G′, which has 1 less edge than G.

This concludes the proof of Trémaux’s theorem.

§ 3. Tarry’s solution.

We can solve the labyrinth problem in a rather simpler way if, instead of the assumptions that form the basis of Trémaux’s solution, we adopt the following assumptions: Every time we arrive at any vertex P it is known for every edge PK ending at P whether it has been traversed in the direction of K; and we can always determine the edge by which P was reached for the first time (the “entry edge” of P).

{42} For this case the problem was solved by Tarry [1]¹. Tarry’s instructions are as follows:

¹ Referring to this work, Rouse Ball [1, p. 207] gives a still simpler “solution”, which however is wrong. Indeed, simple examples show that with Rouse Ball’s procedure it is possible to come to a halt before traversing all the edges. In the same place Rouse Ball restricts the treatment explicitly to two-dimensional labyrinths. This is quite unnecessary. Everything remains valid for e.g. catacombs, where the alleys can run in an arbitrary way under and over one another.

If you come via an edge PQ to a vertex Q, continue the journey along any edge QR that has not yet been traversed in the direction of R; but do not choose QR to be the entry edge of Q unless all other edges QK ending at Q have already been traversed in the direction of K.

By means of this rule it is guaranteed that every edge is traversed at most once in either direction, and thus at most twice in all. Just as for the Trémaux journeys above, so it follows here that the journey must break off sometime, and that this can happen only when you arrive back at the starting-point A₁ of the journey. We shall now prove Tarry’s theorem, which states that when the journey is broken off, every edge has been traversed twice, once in each direction².

² The first part of the following proof is due to Tarry.

Let A₁,A₂,A₃,… be the vertices of the journey, in the order in which they are [first] visited. It is clear that all the edges A₁K ending at A₁ have already been traversed in the direction of K, for otherwise the journey could not have broken off at A₁. Since A₁ has been reached as many times as it has been left, every edge A₁K must also have been traversed in the direction of A₁. We show that the edges ending at the remaining vertices A_n have also been traversed in both directions. If this were not the case, the sequence A₁,A₂,A₃,… would have a first point A_n such that some edge A_nK had not been traversed twice. Since A_n has also been left as often as it has been reached, there must be both an edge A_nK₁ that has not been traversed in the direction of K₁, and an edge A_nK₂ that has not been traversed in the direction of A_n. But now, for the entry edge A_αA_n of A_n, we certainly have α<n, so that A_αA_n (like all edges ending at A_α) has also been traversed in the direction of A_α. But, according to Tarry’s rule, this is regular only if all edges A_nK ending at A_n have been traversed in the direction of K. And this {43} contradicts the fact that A_nK₁ has not been walked in the direction of K₁.

It remains only to show that every point of the graph is one of the points A_i, and has thus been visited during the journey. Let us assume that a vertex B has not been visited. We join B to A₁ though a path A₁B₁B₂…B_ν (B_ν=B). Let B_α be the first point in the sequence B₁,B₂,… that has not been visited during the journey. Then B_α−1 has been visited (if α=1 we set B_α−1=A₁), so that, as we have seen, B_α−1B_α has been walked (indeed twice). Thus B_α has also been visited, contrary to our assumption.

This concludes the proof of Tarry’s theorem.

§ 4. Connection between Trémaux’s solution and Tarry’s solution.

Between Trémaux journeys and Tarry journeys there is an interesting connection, which is expressed through the following theorem:

Every Trémaux journey is also a Tarry journey¹.

¹ See the Remarque by Tarry [1, p. 190].

In other words, we shall now prove the following:

If during a Trémaux journey you arrive at a vertex P, which is distinct from the starting-point of the journey, then the journey will only be continued along the entry edge of P if all other edges PK ending at P have already been walked in the direction of K.

This is clear, if P is reached for the first time, so that P is an endpoint of the graph; we can thus assume that this is not the case. We shall denote by ρ_n the number of edges that end at P and that, after P has been visited for the nth time (n=1,2,3,…), have been walked exactly once. If you arrive for the nth time (n>1) at P via an edge that is being walked for the first time, you must retreat, and thus ρ_n=ρ_n−1. But if this edge has already been traversed once, it now ceases to be an edge traversed exactly once. Thus ρ_n=ρ_n−1−2 or ρ_n=ρ_n−1, according as the edge along which we continue the journey – after arriving at P for the nth time – has also been walked once before or not. From ρ₁=2 it thus follows that ρ₂=0 or 2, and thus also ρ₃=0 or 2, etc.:  every ρ_n is either 0 or 2 (if ρ_κ=0, then of course ρ_κ+1=ρ_κ+2=…=0).

{44} Let us now assume that after the nth arrival at P, via the edge Q_nP (n>1), the entry edge Q₁P of P has been chosen as the continuation of the journey (we have Q_nP≠Q₁P since otherwise, because of n>1, Q₁P would be walked three times). After the (n−1)th passage of P, both Q₁P and Q_nP have already been walked. For Q₁P this is clear, since n>1. For Q_nP it follows from the fact that otherwise, after the nth arrival at P, instead of choosing PQ₁ you would have had to retreat via Q_nP. On the other hand, before the nth arrival at P these two edges have been walked only once, for otherwise the walking of these edges during the nth passage through P would not accord with Trémaux’s rules. Therefore, since ρ_n−1 cannot exceed 2, ρ_n−1=2. Thus, before the nth arrival at P, among all the edges KP only Q₁P and Q_nP have been walked exactly once, while the other edges ending at P have been walked twice, since if one of them had not been walked the choice of the already-walked edge PQ₁ after the nth arrival at P would not be regular. But according to Trémaux’s theorem no edge can be walked twice in the same direction; so that, with the exception of PQ₁, all the edges PK have been walked in the direction of K. Thus on the nth arrival at P we have that PQ₁ is indeed the only PK that has not been walked in the direction of K.

Here let us add a remark about Tarry’s solution. If one were to modify Tarry’s rule so that, instead of requiring 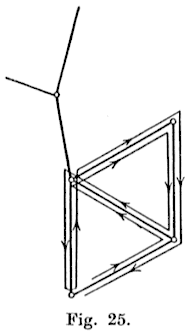that no edge should be walked twice in the same direction, nothing more was asked than that no edge should be walked three times, then the labyrinth problem would not be solved by the new rule. As the journey in Fig. 25 shows, it is then possible for edges to remain unwalked.

Even though, as has just been proved, Trémaux’s rules arise as a specialization of Tarry’s, the result attained through Trémaux’s solution of the labyrinth problem is in a sense more general than through Tarry’s, inasmuch as with Trémaux journeys the requirement of opposite directions is (so to speak) automatically fulfilled, and the direction in which an edge must be walked on returning to an endpoint of that edge need not be assumed known.

{45}

§ 5. Reversed journeys.

Finally, two further remarks will be made, concerning the reversal of a journey. For both of these I am indebted to the kind communication of J. Kürschák.

If

A₁A₂ … A_μ−1A_μA_μ+1 … A₁(I)

is a Tarry journey, so also is the reversed journey

A₁ … A_μ+1A_μA_μ−1 … A₂A₁.(II)

Indeed, it is clear that the (completed) Tarry journey is characterized by the following three properties:

1. No edge is traversed twice in the same direction.

2. The entry edge of any vertex P is identical with the exit edge of P, along which P is quitted for the last time (otherwise, contary to Tarry’s theorem, this entry edge would be traversed only once).

3. All edges are traversed in both directions (this is Tarry’s theorem).

Now (II) obviously has every one of these three properties, provided that this is true of (I).

The correcponding result also holds for Trémaux journeys. Indeed, we prove the theorem:

If (I) is a Trémaux journey, then so also is the reversed journey (II).

We must show that in journey (II) the transition from A_μ+1A_μ to A_μA_μ−1 satisfies Trémaux’s rules. – If in this transition A_μ is visited for the first or last time, then this transition satisfies Trémaux’s rules provided it satisfies Tarry’s (even when A_μ is an endpoint of the graph). But this is certainly the case, since (I) – as a Trémaux journey – and thus also (II) – as the reversal of a Tarry journey – are Tarry journeys. We need therefore only take account of the case where in the transition from A_μ+1A_μ to A_μA_μ−1 the point A_μ occurs neither for the first nor for the last time. Here two cases are to be distinguished. Firstly let A_μ+1A_μ=A_μA_μ−1. Then, since every edge is walked only twice, this edge has not been walked before. The retreat along this edge therefore satisfies Trémaux’s rules. Secondly let A_μ+1A_μ≠A_μA_μ−1. On the corresponding transition from A_μ−1A_μ to A_μA_μ+1 in (I) A_μ is then likewise reached neither {46} for the first nor for the last time. On this transition therefore (α) A_μ−1A_μ has already been walked for the second time (for otherwise you would have to retreat at A_μ) and (β) A_μA_μ+1 only for the first time. Indeed, if A_μA_μ+1 had been walked for the second time, then on this passage of A_μ the number ρ of edges ending at A_μ and walked exactly once would be decreased, and thus – as we saw above – be equal to zero, and this is impossible, since – in view of the fact that the Trémaux journey is at the same time a Tarry journey – the entry path of A_μ remains walked exactly once until the last passage through A_μ. But now (α) and (β) imply that in (II) on the transition in question A_μ+1A_μ is walked for the second time and A_μA_μ−1 for the first time. And this accords with Trémaux’s rules.

Let {A,B,C,…} be a set of “points”. If one joins certain pairs, each consisting of two distinct points of this set, by one or more “lines”, the resulting system is called a graph. Those of the points {A,B,C,…} that are joined to at least one point are called the vertices [Knotenpunkte] or points [Punkte] of the graph (vertices that one might call “isolated” are thus excluded). The inserted lines are called the edges [Kanten] of the graph¹).

¹) In this sense the word graph seems to have been first used by Sylvester [3, p. 149] in 1878. As a short, suggestive term that can be used in all languages it seems to us the most appropriate. In the same or similar sense the following expressions are also used: Linearkomplexion, Liniensystem, Streckenkomplex, Kantenkomplex, Netz. The French very often use réseau. For Knotenpunkt the following have become established in English: node, knot, vertex; in French: sommet, nœud, carrefour; and for Kante in English: branch, edge; in French: chemin, arête, lien.

In the definition of a graph we have assumed that every edge joins two distinct points with one another. It is often convenient to treat graphs in the broader sense, i.e. to allow also those edges that join a vertex to itself. Such an edge is called a loop [Schlinge] and can be denoted by PP.

Theorem I 1: A set Π of points and a set Κ of edges form respectively the set of vertices and the set of edges of a (necessarily unique) graph, if and only if the endpoints of every edge in Κ belong to Π and every point of Π is the endpoint of an edge in Κ.

If all the edges of a (finite) graph can be enumerated in a sequence of the form

AB,BC,CD,…,KL,LM(1)

where every vertex and every edge can occur any (finite) number of times, then the graph is called a chain. According as A≠M or A=M, the chain is called open or closed. In the first case we say that it joins the vertices A and M, or again, that A and M are the endpoints of the open chain. The remaining vertices, and all the vertices of a closed chain, are called inner vertices. If an edge oocurs n times in (1), then n is called the multiplicity of this edge w.r.t. the chain. We clearly have

Theorem I 2: The sum of the multiplicities of all edges of a chain that end in the same vertex P is even or odd, according as P is an inner vertex or an endpoint of the chain.

If in (1) no edge occurs twice, i.e. if every multiplicity is 1, then the chain is called an (open or closed) walk.

If further the points A,B,…,L,M are all distinct from one another, then the open walk is called a path; if A=M but A,B,…,L are all distinct from one another, then the closed walk is called a cycle.

Theorem I 3: If certain edges of a graph form an open chain that joins the vertices A₁ and A₂, then certain edges of this chain form a path that likewise joins the vertices A₁ and A₂.

Theorem I 13: If in a connected graph G there is a path W that joins the endpoints A and B of an edge AB and does not contain this edge AB, then the graph G′ that results from the removal of the edge AB from G is likewise connected.

Theorem I 14: If one removes from a connected graph G one of its end edges (dead ends) or an edge of one of its cycles, then the remaining edges still form a connected graph G′.

Here it is convenient to introduce the notion of graph addition. Let {G_α} be any set of graphs. By Theorem 1 the vertices and edges that are contained in at least one of the graphs G_α form a graph G. If the graphs G_α are pairwise disjoint, then we call G the sum of the graphs G_α and write G=ΣG_α. The assumption that the G_α are disjoint is essential here; only in this case do we say that a graph separates into subgraphs G_α, and only in this case do we write equations of the form G=ΣG_α.

Theorem I 24: A graph is connected if and only if it is not the sum of two proper (non-empty) graphs.

Theorem II 5: Every finite connected graph G can be traversed as a closed chain such that every edge is traversed exactly twice.