Journal of the Antiquarian Association of the British Isles, 2, 65–71 (June 1931)
A reply to R. C. Dunt’s article “Local markstones, roads and trackways” in the March issue of the same journal. Watkins tries to show, by rough statistical arguments, that alignments of ancient sites cannot all be accidental.
In the 1982 edition of British Geomantic Pioneers the editor changed “alignment” to “alinement”, the spelling that Watkins preferred.
{65}
by alfred watkins, f.r.p.s.
NINE years’ experience, working and writing on mark-stone, mound and track alignment, tells me that to give (in response to references in the March number of this journal), a condensed outline of conclusions, is to invite a repetition of accusations of vain and illogical imaginings, in spite of a great mass of confirmation by other field observers.
This contribution will, therefore, be confined to seeking a logical basis for examination of observed facts, very dull but necessary.
The proof is chiefly to be found in the fact of certain classes of what are now called “Ancient Monuments” aligning with each other, and in fragments of present-day roads or paths being occasionally found on such track-lines; in some cases, however, the alignments have no indication of having been made for track purposes.
The deduction of an organised system of straight tracks in prehistoric Britain is denied by many critics, who put it down to imagination and accidental coincidence, and infer that the theory was formulated first, and facts then selected to fit it. This inference is not correct in my case, for it was not until a large number of alignment facts had been observed, that any theory or outline for further investigation was formed as a deduction.
{66} The basic fact to be faced—and this paper is written to face it—is whether these mark-points or “monuments” (mounds or standing stones, or some other structure evolving from them on the same site), were designedly placed in line by man, or whether such alignment can be accidental. The investigation will also be useful as applied to the seasonal alignments found in stone circles and dolmens by Lewis, Lockyer, and Boyle Somerville, and to the profuse alignment found in prehistoric cup-markings. It is in fact a dip into mathematics, and is necessary, for I have found well-meaning believers in the old straight track present weak instances which can be explained by accidental coincidence.
Begin then with two points, A and B, marked at haphazard on a sheet of paper.
Any argument that these fall on a straight line, A—B, is valueless, for a straight line can always be drawn between any two points. Remember, therefore, that two points must always be deducted from the number of any series of mark-points in alignment, and that it is only the number in addition to the first two which can be counted as tending to prove the alignment.
Now close the eyes, and, turning the paper round to make the position of A and B unknown, mark at haphazard a third point, C.
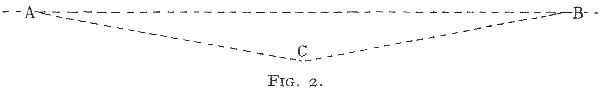
The chances are vastly against C being in exact alignment between A and B, thus:—
But if—in actual cases in the field—such three points do fall into alignment, the problem is: what is then the chance of its being an accidental coincidence? and this is what I now roughly investigate by the diagrams, going back to Fig. 2.
{67} Consider A as the centre of a circle, and that C might be on any line radiating from it in any direction on the sheet; that we will only treat it as being in alignment if it falls within a quarter of a degree in angle (this a rough estimate of an average working limit of error) from the line A—B. There are 1,440 quarter degrees to the circle: C has two chances of coincidence, one on each side of A. With this limit of error, therefore, the chance of C falling accidentally into alignment on the line A—B seems to be one in 720.
The addition of C however, makes available the additional lines A—C and B—C, which afford opportunities for the third point (not being a terminal of these new lines) to align on them by accidental coincidence, having the same chance that C had.
The total chance of a three-point alignment when only three mark-points are available, seems to be three in 720, that is, one in 240. To put it in a table:
| A | has a chance | to align on | B—C. |
| B | ,, | ,, | A—C. |
| C | ,, | ,, | A—B. |
There are almost always more than three mark-points present on the area investigated in actual field work. The chances of accidental alignment by coincidence increases with each point added to the first three, this a rapid increase by geometric, not arithmetic, progression; but I do not attempt to work out the formula.
In the diagram below I add a fourth point, D.
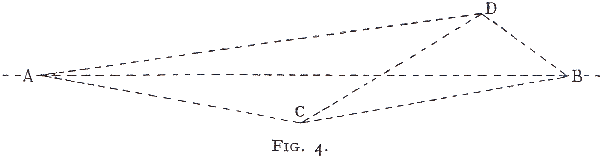
The adding of D provides three new lines available for accidental coincidence. It greatly increases the chances of three-point alignment.
{68} The following table shows these additional chances, nine in all:
| A | has additional chances | to align on | C—D and B—D. |
| B | ,, | ,, | A—D and C—D. |
| C | ,, | ,, | A—D and B—D. |
| D | ,, | ,, | A—C, B—C, and A—B. |
Four mark-points on a given area have, therefore, a total of twelve chances for accidental alignment compared with three chances for three-points. That is, twelve chances of one in 720, which is one chance in sixty, instead of one in 240.
Now to estimate (crudely), the chances of an alignment of four points with only those four on the sheet. This is, I think, very remote, for the one point left from the three which are already on a line has only one line and one chance left available, that is, a 720th of one-in-sixty, which makes a chance of one in 43,200. Experience with a large number of haphazard trials on sheets of paper confirm this. The result (if this comes off), is as below:—
I now pass on to a series of rule-of-thumb trials which I made for larger numbers of mark-points on one sheet of paper. They were marked (with the eyes shut), by small crosses, the paper turned between each mark. I usually made ten trials with each number and took the average result.
| With 6 points, 40% of the trials had ONE alignment of three points. |
| With 9 points, 95% of the trials had ONE alignment of three points. |
| With 10 points all trials had ONE alignment, and some two. |
But in many scores of trials as above I only found ONE case of a four-point alignment.
In many cases in practice—on map or in field-work—the number of mark-points available in the area is greater than in the above trials.
{69} For example, the ANDOVER Sheet of the Ordnance Map (No. 283, old engraved series, 1-inch scale), contains 51 churches, practically all ancient ones. I must not here give full reasons why most rural churches can be classed with prehistoric mark-points, being evolutions from such on the old sites.
I first tested how far the actual sites on the above map fell into alignment. I found 30 cases of three churches in line, seven cases of four in line, and one case of five. Then to test how much of this was accidental coincidence: on a blank sheet I marked (haphazard all over the sheet as before), 51 X’s. In these I found 33 cases of three in alignment, and only one case of four. Repeated tests with numbers up to 100 points on a sheet gave similar results, the number of three-point alignments increasing greatly with more points, but four-point alignments remaining very scarce. In tests on maps of actual prehistoric sites, whether of mark-stones, ancient mounds or churches, or all together, cases of four, five, and even six or seven points in line are quite frequent.
The net deduction from these trials is that even with a small number of mark-points, cases of three points in alignment are practically worthless as evidence, and that they are found as accidental coincidences in great number when many mark-points are in the area. I regard a clear case of four-point alignment of ancient sites to be a fair assumption, but short of absolute proof, of the alignment having been man-designed.
I regard a cross-country alignment of five good mark-points, or of four with good confirmation by existing tracks, as being proof (beyond possibility of accidental coincidence), of a man-designed alignment.
The presence of stretches of present-day straight track on an alignment under investigation can be taken as contributory evidence, but not as strong as a prehistoric mark-point, it being very difficult to judge the antiquity of such bit of track.
It is of course impossible that any stretched line or straight rule could have been used for laying out any track of the length we discuss. A sighting method was inevitable, and the authorities on “Roman” roads not only assume this, but describe the means used, {70} such as the pair of staves, the Groma (with plumb-line), smoke signals, and sighting mounds. It is a strange feature of modern archæology that these same experts illogically pour scorn on any assumption that earlier races than the Roman could have used similar methods for road making.
I must close this contribution by reproducing from The Ley Hunter’s ManualScanned from the clearer copies in Alfred Watkins, The Old Straight Track, Figures 3–6. (Simpkin Marshall, 2s.), some diagrams of actual track-alignments, without stopping to give full explanations.
In the first (South Radnor Mounds), the one line passes through four mounds, two small “camp” earthworks, and two churches. The other line through three mounds or moats, a church, a hill-top, and a terminal hill-top with a beacon name.
In the second (Pilleth Mounds), the one line passes through three mounds and a church; the other through four mounds.
Both the above pairs of lines cross at a camp or earthwork, and {71} they take in almost all the “monuments” (of the types mentioned), within a mile; the extra ones being marked.
The next diagram (Cotswold), has fewer mark-points, namely: two churches, Sunrising Hill-point, and an ancient ford—but it is also the backbone of a dozen miles of present track, which repeatedly diverges a little, and then comes back. A topographical book of the district says that this cart-road is marked with several upright stones.
The bottom (Church) diagram aligns through three ancient church sites of the city, and one mounded-up site with the significant name of Crozen, and the reputation (from the statement of an antiquary who lived there long ago), of having been a “Saxon burial ground.” It also lies on two streets, the longer one for half a mile, it being interesting to note how the road obviously swerves to one side to avoid the Chapel (a Templar’s Round Church) and the Crozen sites, and comes back into line.
It is of course essential to the proof of a system of prehistoric tracks over mark-points, that the points quoted as proof should really be prehistoric in origin, or the sites of such. The most careful observer will make an occasional slip in this, but it is not fatal to the remaining proof.