C. W. Dymond, “The megalithic antiquities at Stanton Drew”
Journal of the British Archaeological Association, 33, 297–307 (1877)
{297}
THE MEGALITHIC ANTIQUITIES AT STANTON DREW.
by c. w. dymond, esq.
“remnants of things that have passed away:
fragments of stone reared by creatures of clay.”1
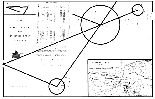
Dymond’s plan
The megalithic antiquities at this place, which rank
third in importance among works of this class in England,—viz.,
after Avebury and Stonehenge,—have often been described, and, as
usual, their arrangement and purpose have been fruitful subjects of
speculation. An attentive examination of these remains, some years ago,
convinced me that certain theories regarding them were based upon
erroneous assumptions, originating in the data given by the survey made
in 1826 by Mr. Crocker, which is the basis of most of the published
plans, and has been regarded by the principal writers on the subject as
the best, and, at the same time, as a trustworthy authority. Hence, I
was led to make a new survey2 on a much larger scale, in
which scrupulous care has been taken to insure the most minute accuracy
in every part, and to map everything that could be found after an
exhaustive search. By the kind aid of the vicar, the Rev. H. T.
Perfect, and of Mr. S. B. Coates, of the Manor House, the positions
of several stones which had been entirely buried—probably for
generations—were ascertained, and their contours traced with a
probe, where they could not be exposed by the spade. These—which
are all that are now known to exist—have been included in the
plan, which gives the large circle twenty-four stones, being ten
more3 than are shown in Crocker’s survey, and six more
than are mentioned by Rutter, who, in his Delineations of
Somerset, 1829, describes five stones as standing erect, eight
others as “evidently buried just below the surface, whilst the
position of five more is indicated in dry summers by the withering of
the turf over them”. The plan in Seyer’s History of
Bristol, 1821, shews fourteen stones standing or lying distinctly
above-ground, eight others as nearly buried, and five more as merely
conjectural or “only suspicious”. All of these have been
found,
{298}
except three,—one of them being that which he has placed at the
root of the southern line of the large-circle avenue, and has indicated
as partly visible; the other two being in the last class,—one of
them supposed by him to be between Nos. 6 and 7, and the other to be
between Nos. 14 and 15. Repeated search has made it clear that these do
not exist, and, probably, did not in Seyer’s time, for old
inhabitants of the village testify that none have been removed within
their memory. As to the first-mentioned,—that at the entrance to
the avenue,—he must have been misled by the small fragments which
abound in that part of the field in a layer a few inches below the
surface, and which may be the remains of a stone, long ago broken up. In
the south-west circle, Seyer has shown a partly-visible stone about
half-way between Nos. 6 and 7. It is not there now, and, possibly, its
remains may exist in the fragments at the corner of the wall, near the
centre of the circle.
The general results of the inquisition into the sixty-six stones now
remaining at Stanton Drew, as numbered on the plan, may be tabulated
thus:—
| | | Prostrate Stones |
| |
| Large circle | 3 | 15 | 6 |
| Ditto, ditto, avenue | 3 | 2 | — |
| North-east circle | 5 | 4 | — |
| Ditto, ditto, avenue, etc. | 5 | 5 | — |
| South-west circle | — | 12 | — |
| The Cove | 2 | 1 | — |
| Lower Tynings | — | 2 | — |
| Hauteville’s Quoit | — | 1 | — |
| Totals | 18 | 42 | 6 |
With regard to the original number of stones that may have composed
these circles, it is only in the case of the large one that there is
room for much difference of opinion. The number (eight) remaining in the
small one is, evidently, complete. One appears to have been removed from
its proper position in the south-west circle, which pretty clearly
contained twelve stones in its pristine state. The distances between
those remaining in the large circle are so irregular—varying from
11 ft. to 107 ft.—that it is impossible to allocate most
of the missing stones with any assurance of accu-
{299}
racy. There can, however, be no reasonable doubt as to one,—that
at the root of the southern line of stones of the avenue,—and the
wide gaps between Nos. 6 and 7, and Nos. 14 and 15, must almost
certainly each have been broken by at least one stone. If these are
supplied, a readjustment to nearly uniform intervals of nine out of the
fifteen fallen stones will give eighteen intervals, varying only from
42 ft. to 46 ft., and will leave eight intervals, which cannot
well be adjusted, varying from 29 ft. to 61 ft. But, although
it seems highly probable that this circle, when complete, consisted of
twenty-seven stones, it by no means follows that these were generally
spaced at tolerably regular distances, as it is quite clear that they
were not so in some parts of the circle.
Rutter describes the large circle as separated from the river “by
some rising ground, forming a sort of rough amphitheatre”. Nothing
of the sort now exists, or, probably, ever did; for distinct traces of
anything of this kind, whether natural or artificial, are scarcely ever
obliterated; and he must have magnified to this degree the gentle slope
which runs up toward the circle, unless he refers to the line of a
former hedge and ditch which crosses the avenue of the small circle.
An important point, in which Crocker’s plan seems to have misled
antiquaries, is the shape and size of the large and south-west
peristaliths. The diameters have been taken between the stones as they
stand or lie; but no one seems to have studied on the spot how they
fell, so as to discover where they must have originally stood. The plan
which accompanies this paper shows the results of a careful inquiry into
this matter, demonstrating that, when these peristaliths were perfect,
they were very nearly true circles. Thus, all speculations based upon
their supposed ellipticity fall to the ground.
With respect to the alignment of the remains, it is noticeable that the
centre of the south-west circle, the centre of the large circle, and the
quoit, are nearly in one straight line; and that the centre of the
north-east circle, the centre of the large circle, and the centre of the
Cove, are still more nearly in another straight line. This may be merely
a coincidence; but, if the like be observed in other instances, it may
lead to some discovery of interest. To ascertain whether all
{300}
the leading points could be seen from one another, if there were no
trees or buildings in the way, I took a great number of levels over the
whole area occupied by the remains, and, from these, have contoured the
parish-map, attached to the larger survey, with lines showing
differences of 5 ft. in height. Some calculations, based upon
these, will be found among the memoranda at the end of this paper, from
which it will be seen that every such point could be seen from every
other, even in the most difficult case, by standing a very few feet
above the ground. I am, however, disposed to attribute very little
importance to this fact, as it is probable that, in early times, this
valley was even more wooded than it is at present, so that then, as now,
it would be difficult, if not impossible, to keep some of these stations
respectively in view.
As to the alleged great reduction in the size of Hauteville’s
quoit, it appears to have been less injured than has been generally
believed. It is true that Stukeley, in 1723, made it 13 ft. by
8 ft. by 4 ft.; but that these figures were greatly exaggerated,
is evident from the statement of the careful Aubrey, in 1664, who gives
the dimensions of the quoit as 10 ft. 6 ins. by
6 ft. 6 ins. by 1 ft. 10 ins.,—though he
himself did not measure it, but got a friend on the spot to do it for
him. If his figures were correct, the stone has since lost only about
3½ ft. of its length.
There has been much speculation as to the group of stones at the root of
the southern line of the avenue of the northeast circle,—some
supposing that they are the ruins of a dolmen, and others, that one of
them was a menhir. No. 18 is still well founded in the ground, and
evidently in sitû, though it is far from being upright; and
a careful comparison of its side next No. 16, with the recessed part
of the latter, with which it perfectly corresponds, must convince
everyone who closely examines them that they were formerly one stone,
which thus stood nearly behind No. 1, but, perhaps, 2 ft. or
3 ft. more to the north. The small stone leaning against the western
end of No. 16 was, I think, attached to it, as its original base;
and thus these three stones are disposed of, and formed a fine monolith,
which must have overtopped the others. The fragments, numbered 19 on the
plan, are sunk into, and are nearly level with the ground, so that it
can only be conjectured that they are parts of what was
{301}
formerly one stone, then standing on the northern side of No. 1,
which is much smaller than any other of the stones in this circle, and
seems to need some sort of reinforcement to balance them.
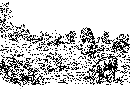
N.E. circle
This small, or north-east, circle, and the groups of stones on both
sides of it, have been a battle-ground of contending archæological
factions,—some stoutly holding to the opinion that here we see the
remains of what once were two concentric circles; others say three; and
others, again, conjure up no less than five. Some see in the outlying
stones a sharply-curving avenue; and others assume that the alignments
were always nearly as they now are, and hold that the avenue of the
large circle was intended to point toward the isolated stone, No. 14
in the north-east group. Now, it may be asserted that, if we scale on
the plan, from the centre of the north-east circle to the stones
numbered 24 and 27 in the large-circle avenue, and to No. 13, and to
the western end of the fallen No. 11 in its own avenue, we shall
find the distances (124 feet, 130 feet, 133 feet, and
132 feet) sufficiently alike to warrant us in making these the
remaining members of an outer peristalith. I will cheerfully make a
present of this approximation toward concentricity to those who can make
anything of it,—at the same time asking them to explain how it
occurred that, of all the stones which must have formed these concentric
rings, those only have been left which happen to be ranged in straight
lines, and now form distinct avenues leading to their respective
circles; and also why, in this case, the usual rule was reversed, which
placed the finer stones outermost and the smaller within. The theory
that there was one sharply-bending avenue connecting the two circles
does not look much more tenable, for, not only is it very rare to find
two circles united in this manner, but it is not likely that those who
designed these structures, if their wish was to make a passage
connecting the circles, would have taken so indirect a way, especially
when it involved a considerable descent, and subsequent ascent. It has
been generally noticed that the stones in such avenues diminish in size
as they recede from the structures at their roots; and the same custom
seems to have been roughly followed here. It is thus probable that these
two avenues were always quite distinct, converging toward one point; and
that the larger
{302}
one was formerly longer, terminating, as to its northern line, in the
small stone, No. 14, though no trace of the foundations of any
intervening stones has been found. Possibly we have here the ruins of
works of different dates; and, if so, it is the more easy to understand
why particular members, such as these avenues, should have been repeated
in the later portion of the work without having necessarily any direct
connexion with the earlier.
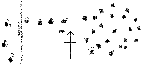
Aubrey’s plan
The strongest, indeed the only evidence as to the existence here of
concentric circles is afforded by the plan which Aubrey made
when he visited the spot in 1664, and which illustrates Part I of his
manuscript work, Monumenta Britannica, in the Bodleian, a
facsimile1 of which accompanies this paper. In his account of
it he says:—
“This Monument is bigger than Stoneheng: the Diameter is ninety
paces. I could not percieve any Trench about it as at Stoneheng, etc.:
it is in ploughed land, and consequently easily worne out. When I last
sawe this, it was in Harvest time, and the Barley being then ripe, I
could not come to survey the stones so exactly as I would otherwise have
donne: but this scheme (as it is) resembleth it. The stones a a a a
etc: seeme to be the remainder of the Avenue as at Aubury, and
Kynet, the length of the Avenue is about halfe a quarter of a mile: and
the stones d d d might be a [line] leading to another Temple; as
from West Kynet to the Temple on the top of the Hill. see the
scheme.”
Aubrey was unfortunate in the time of his visit, and evidently acquired
a very confused notion as to the arrangement of the different parts of
the work: for, seeing the rude stones rising in every direction out of a
sea of corn, he might well imagine (what his whole work shows he was
always ready to find) concentric circles surrounding a central stone.
Except by some such explanation of his plan as follows below, his
dimensions cannot be reconciled with anything that now
remains—e.g., the diameter of ninety paces (225 ft.)
with the diameter of the small circle (97 ft.), or with that of the
large one (368 ft.); the length of the avenue of “half a
quarter of a mile” (220 yards), with the extreme distance
(108 yards) from the root of the large-circle avenue to the
extremity of the small one.
After much study of his plan, I think it may be thus explained. Assuming
that he is right in his compass-bearings,
{303}
and taking for a guide the old hedge which he has shewn,—the line
of which is still visible,—we shall find the three stones,
d, d, d, shown in a curved line, matched
by stones numbered 8, 9, and 13 of the large circle; the four stones,
a, a, a, a, on one side of
his avenue, by those numbered 16, 18, 19, and 20 in the large circle;
the single stone, a, on the other side of the avenue, by
No. 21 or 22 in the large circle; the single stone outside his
circular group, by No. 23 (the two stones outside the same, which
he has crossed out, were probably at first intended to represent Nos. 23
and 25); and then,—omitting Nos. 12 and 14 of the north-east
avenue, which are small, placed low, and, probably, at the time out of
his sight behind another old hedge,—we shall have nineteen stones
in the remainder of the two avenues, and in the circle, to satisfy the
number, nineteen, which he has shown in his concentric plan. Moreover,
we shall have them extending, over a piece of ground ninety paces
across; and, from the end of this measurement to stone
No. 8,—the extremity of his supposed curving avenue,—we
have a distance of 233 yards, which is only 8 yards over the
length he has assigned to the avenue. By what other mode of explanation
can we account for his omission of all the stones of the smaller avenue,
and for his representing the number and direction of those in the larger
one so erroneously? If we could but surmount this difficulty, we might
be tempted to seize upon a peculiarity which, at first sight, promises
to give a clue to the labyrinth, and that is, the pictured plan of one
of the outer stones on the south side, as though intended to represent
the pointed and leaning stone, No. 2, in a similar position in the
north-east circle, or, as it might be thought, the leaning stone,
No. 18, with No. 16 lying at its foot. But, if so, then he is
wrong again in showing twelve (or, possibly, eleven) stones in this
outer ring against eight, the present, and evidently complete number,
within which he shows six (or, possibly, seven) in an inner ring, and a
monolith in the centre. It would be very singular if all these stones of
the inner circle have been removed, without leaving any trace of their
site, while all the outer ones have been allowed to remain. Nor will it
do to suppose his inner ring to represent the existing one, for,
independently of the difficulties discussed above, neither does the
number of stones here agree with those now in and on the ground. On
{304}
the whole, therefore, I think no other conclusion is possible than that
the avenue and curved line of stones shown trending westward and
southward in Aubrey’s plan, represent the stones on the northern
and western side of the large circle (of whose existence, as such, he
does not speak), and that the two concentric circles, with their central
stone, represent his idea of the arrangement of the small circle, its
avenue, and four stones of the avenue of the large circle. It is,
perhaps, a pity that he ever made the plan, as he “could not come
to survey” it better; for it is remarkable how often incorrect
drawings have stirred the embers of strife, and bewildered the patient
student by their fabulous data.
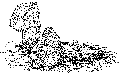
The Cove
The Cove has been another gage of combat. With some it has been a throne
or chair of state for the arch-druid, who was even seen sitting within
its ample arms several times a day to dispense justice! With others it
has been a dolmen. If we suppose the latter, its reconstruction is
attended by the following difficulties:—The prostrate stone (which
could not possibly have fallen, as it has, if it had been the
“table-stone”) must have been a side-stone standing erect
where its southern end now is, and at right angles with the other two,
on the broken stump which still seems to be traceable in the ground. We
shall thus have three uprights of greatly varying height—one
14 ft. 6 ins. high, another 10 ft. 3 ins.,
and a third 4 ft. 6 ins. It would be impossible to rest a
cap-stone on these, as it demands a fourth supporter on the southern
side, nearly, if not quite, as high as the prostrate one. Then, over the
head-stone there will be a gap about 4 ft. high, in addition to the
large square hole on one side of its base; and, over the foot-stone, a
gap 10 ft. high, increased by the pyramidal shape of the stone.
Now, not only would such a dolmen be of most unusual height, in
proportion to its length and width, but its chamber would always be open
to easy access, which it would indeed tax the ingenuity of the sternest
unbeliever in “free-standing” dolmens to close by
microlithic masonry, as a necessary preparation for covering it with a
mound. But, if there were formerly a fourth side-stone and a
table-stone, what has become of them? They are not buried in the ground.
There is no reason to suppose that they have disappeared during the
present century; so they are not likely to have been broken up to make
or mend the country lane which
{305}
passes near by; and no fragments of such stones can be seen in any of
the neighbouring fences or buildings. The most reasonable conclusion,
then, seems to be, that these three stones are all that this monument
ever possessed; and it is fortified by the fact that two instances of a
similar kind formerly existed at Avebury.
In this paper, as well as in the following memoranda, I have
endeavoured, as much as possible, to avoid repeating what others have so
well said before. My object has simply been to make a contribution to
our knowledge on the subject; and, if these remarks, and the survey
which accompanies them, should throw any fresh light upon it, the labour
which has been spent on them will not have been bestowed in vain.
MEMORANDA WRITTEN ON THE ORIGINAL PLAN.
These remains are situated in a broad, rich valley, about six miles
south of Bristol, overlooked on the north and south by high hills, and
consist of three peristaliths, two of them with attached avenues; a
group of three large stones, called “The Cove”; two
prostrate stones in a field at the distance of about two thirds of a
mile to the west of the circles; and one prostrate stone called
“Hauteville’s” or “Hackell’s Quoit”,
about one third of a mile to the north-east of the large circle.
This plan has been constructed with the utmost care, from an accurate
instrumental survey. The magnetic bearings were taken with a prismatic
compass, the readings of which were adjusted by angular observations
with a sextant.
The centres of the circles have been fixed by trial, after the plan was
plotted, and indicate, as closely as it is now possible to discover, the
centres of the work as it stood when perfect. To this end, the position
of every stone has been studied on the ground, and, where practicable,
the part which was either certainly or apparently the base of each has
been marked by a small cross. As a rule which admits of but few
exceptions,—and those are accounted for by the form of the
ground,—that end of a stone which is now the lowest, and is sunk
more or less into the ground, was undoubtedly the original base. Where
it has been difficult to choose between two sides, a cross is put to
each, and it is altogether omitted in cases where it has been impossible
to decide on its proper place. From these centres dotted circles have
been struck, representing as closely as possible the lines on which the
stones appear to have been originally set up. It is thus made evident
that these rings were not, as has hitherto been supposed, ellipses of a
greater or less degree of eccentricity; but that, when perfect, they
were very nearly true circles.
The stones which are still erect are filled in with black on the
plan.1
{306}
Two of these in the north-east circle incline from the upright, and one
in the Cove projects considerably beyond its base. The overhang is shown
in outline, but is not shaded. The visible portions of prostrate stones
are stippled and line-shaded, and those parts which are completely
buried are indicated by dotted outlines. Some of these were exposed by
the spade. The remainder were carefully probed to a depth of more than
12 inches, within which depth most of them lie; and it is believed
that in almost every instance the edges have been correctly plotted, and
that no unmeasured stones remain.
Traces of a buried stone, as dotted in the plan,—probably the
broken base of the prostrate stone,—were found at the rear of the
Cove, the site of which, between and around the stones, appears to be
formed of small stones rammed together; probably, as is usual, for the
purpose of keeping the erect stones in position. Nothing of the kind has
been detected in connection with the circles and avenues.
The large and north-east circles stand in a
posture
sloping very gently
toward the stream on the north. A rather sudden fall eastward occurs at
about the middle of the avenue of the north-east circle. From the large
circle the ground rises rather more steeply toward the south-west
circle, which is on a level platform of its own diameter. From this the
ground declines in every direction,—very gently toward the west
and north-west, and most steeply toward the east. The Cove stands on the
brow of a small flat elevation of nearly equal height, level to the
north-east, as far as the church (which stands near its edge), declining
very gently toward the east and south-east, and most steeply toward the
west.
If the country were bare, the undermentioned points would be visible
from one another: stones in Lower Tyning, from base of Cove; from
1½ feet over centre of large circle, and from 8 feet
above ground at quoit; centre of south-west circle from base of Cove;
centre of northeast circle from 5 feet high at Cove; centre of
large circle from 6 feet high at the same:—centre of
south-west circle from base of quoit; centre of large circle from height
of 5½ feet at quoit; and centre of north-east circle from
height of 7½ feet at the same:—centre of large circle
from height of 6 feet at centre of south-west circle; centre of
north east circle from height of 4 feet at centre of south-west
circle.
The magnetic bearings, etc., of the avenues are as follow:
north-east circle.
North line of stones bears E., 13½°S., and points 31 ft.
N. of centre of circle.
South line of stones bears E., 8⅓°S., and points 9½ ft. S.
of centre of circle, and 4 ft. N. of stone No. 1, running
through the base of Nos. 16 and 18 when in sitû.
Centre line of avenue bears E., 11°S., and points 11 ft. N. of
centre of circle.
large circle.
North line of stones bears N., 65°E., and points to centre of
circle.1 (?)
{307}
South line of stones bears N., 75°E., and points 6 ft. N. of
centre of circle.
Centre line of avenue bears N., 70°E., and points 3 ft. N. of
centre of circle; or centre line of avenue bears N., 73¾°E.,
and points 19 ft. N. of centre of circle, if the northern line of
stones took the direction suggested in the note below.
Hauteville’s Quoit was formerly larger than it now is. In 1664,
Aubrey measured it, 10 ft. 6 ins. by
6 ft. 6. ins. by 1 ft. 10 ins. In 1723,
Stukeley (probably exaggerating) states its size as 13 ft. by
8 ft. by 4 ft.
Stone No. 16, in the avenue of the north-east circle, now
prostrate, was part of a menhir, of which another part (No. 18)
remains standing, though much declined from the perpendicular. The apex
and south-eastern side of the latter match exactly with the recessed
part of No. 16. The stone leaning against the western end of
No. 16 appears originally to have formed its base, and to have
flaked off when this part of the menhir fell. No. 1 was a separate
stone, and seems never to have been disturbed or injured.
Two of the stones are new red sandstone,—the rock of the
site;—one is similar to that obtained from Dundry, four miles
north-west; a few are limestone from neighbouring quarries; and the
rest,—forming by far the majority,—are a pebbly breccia of
the magnesian limestone, probably brought from Broadfield Down, six
miles west, or from East Harptree, six miles south.
The distances from the large circle to the quoit, and to the stones in
Lower Tyning, are scaled from the Tithe Map; but the magnetic bearings
of these objects were obtained from data observed on the ground. Those
bearings recorded on the plan which could not be taken, in consequence
of intervening obstacles, have been trigonometrically calculated from
those which were instrumentally observed.
{Aubrey’s Scheme}
[The
accompanying Plate
of four views, is a reproduction of those
exhibited by Mr. J. T. Irvine, and described above, at p. 249.]
Editor’s Note:
Dymond’s original plan was hung in Stanton Drew church, and virtually ignored.
By 1976, damp and the ravages of time had reduced it to an unrecoverable state.
It is yet another example of valuable geomantic records being ignored
and destroyed by default.