
E. Lucas, Récréations mathématiques, t. I (2ème éd., Paris, 1882), ch. 2, pp. 21–38.
Lucas’s four-volume work, of which two chapters are republished on this website, is one of the classic books on recreational mathematics. In this chapter Lucas provides a translation of Euler’s paper on the Königsberg bridges, and adds some notes on similar unicursal problems.
{21}
Parmi les divers travaux des mathématiciens sur cette branche de la science de l’étendue que l’on nomme Géométrie de situation, on rencontre, dès l’origine, un fameux Mémoire d’Euler, connu sous le nom de Problème des Ponts de Kœnigsberg; nous donnons, d’après les Nouvelles Annales de Mathématiques [4], un commentaire de cet opuscule, qui a paru en latin dans les Mémoires de l’Académie des sciences de Berlin pour l’année 1759 [5], et qui a pour titre: Solutio problematis ad Geometriam situs pertinentis.
1° Outre cette partie de la Géométrie qui s’occupe de la grandeur et de la mesure, et qui a été cultivée dès les temps les plus reculés, avec une grande application, Leibniz a fait mention, pour la première fois, d’une autre partie encore très inconnue actuellement, qu’il a appelée Geometria situs. D’après lui, cette branche {22} de la science s’occupe uniquement de l’ordre et de la situation, indépendamment des rapports de grandeur. Mais quels sont les problèmes qui appartiennent à cette géométrie; quelles sont les méthodes qu’il faut employer a leur résolution? C’est ce qui n’a pas encore été nettement défini. Récemment j’ai entendu parler d’un problème qui paraît se rapporter à la Géométrie de situation, puisqu’il ne contient, dans son énoncé, que des considérations d’ordre et non de mesure; aussi ai-je résolu d’exposer ici, comme un spécimen, la méthode que j’ai trouvée pour résoudre ce problème.
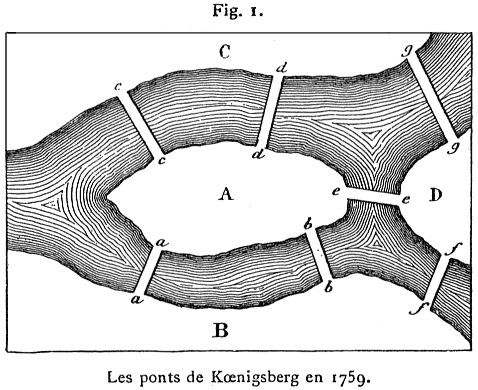
2° A Kœnigsberg, en Poméranie, il y a une île appelée Kneiphof; le fleuve qui l’entoure se divise en deux bras (fig. 1), sur lesquels sont jetés les sept ponts a, b, c, d, e, f, g. Cela posé, peut-on arranger son parcours de telle sorte que l’on passe sur chaque {23} pont, et, que l’on ne puisse y passer qu’une seule fois? Cela semble possible, disent les uns; impossible, disent les autres; cependant personne n’a la certitude de son sentiment. Je me suis donc proposé le problème suivant, qui est très général:
Quelle que soit la forme d’un fleuve, sa distribution en bras, par des îles en nombre quelconque, et quel que soit le nombre des ponts jetés sur le fleuve, trouver si l’on peut franchir celui-ci en passant une fois, et une seule, sur chacun des ponts.
3° Quant au problème particulier des sept ponts de Kœnigsberg, on pourrait évidemment le résoudre en faisant l’énumération complète de tous les parcours possibles; on reconnaîtrait ainsi s’il existe ou non un chemin qui réponde à la question. Mais, par suite du grand nombre de permutations, cette méthode, déjà difficile et laborieuse dans le cas particulier, serait impraticable pour un plus grand nombre de ponts; d’autre part, parmi ces permutations, beaucoup d’entre elles sont inutiles, de telle sorte qu’après avoir terminé l’opération on aurait rencontré un grand nombre de choses qui ne sont pas en question; c’est en cela, sans aucun doute, que réside la cause d’une aussi grande difficulté (1). Donc, en laissant de côté ces considérations, j’ai recherché s’il n’était pas préférable d’imaginer une méthode qui permit de juger, au premier abord, de la possibilité ou de l’impossibilité du problème; je pensais, en effet, qu’une telle méthode devait être beaucoup plus simple (2).
(1) C’est pour la même raison, très probablement, que l’on n’a pas encore trouvé la solution du problème des reines lorsque le nombre de celles-ci dépasse huit; voir à ce sujet notre quatrième récréation sur le problème des huit reines au jeu des échecs. Quant aux permutations qu’il y aurait lieu de considérer ici, ce sont les permutations avec répétition.
(2) Cette remarque d’Euler comporte un très grand caractère de généralité qu’elle ne paraît pas avoir tout d’abord. J’ai observé que, dans un grand nombre {24} de problèmes de la Géométrie de situation, il y a souvent une différence considérable dans la manière de traiter la possibilité et l’impossibilité; en général, l’impossibilité se manifeste plus facilement que la possibilité, ainsi que l’on pourra s’en convaincre dans les théories du solitaire, du taquin et de quelques autres jeux. Dans le paragraphe suivant, Euler ajoute que toute sa méthode repose sur une notation spéciale; nous ferons voir encore que dans tous ces problèmes il en est toujours ainsi. On verra, dans notre récréation sur le jeu de baguenaudier, comment la notation si ingénieuse de M. Gros simplifie considérablement la théorie de ce jeu.
{24} 4° Or, toute la méthode repose sur une manière convenable de représenter les divers chemins; pour cela, je me sers des lettres majuscules A, B, C, D, … pour désigner les diverses régions séparées par les bras du fleuve; alors, si l’on passe de la région A dans la région B, soit par le pont a, soit par le pont b, je désigne ce chemin par AB; la première lettre indique la région de départ, et la seconde la région d’arrivée. Maintenant, si le voyageur passe de la région B dans la région D, par le pont f par exemple, je désigne la seconde traversée par BD, et l’ensemble des deux passages successifs par ABD; ainsi, la lettre intermédiaire B désigne en même temps la région d’arrivée après la première traversée, et la région de départ pour la seconde.
5° Si le voyageur passe ensuite de D en C par le pont g, je désigne l’ensemble des trois passages successifs par les quatre lettres ABDC. Ainsi, la notation ABDC signifie que le voyageur, situé primitivement dans la région A, est parvenu dans la région C, après avoir occupé successivement les régions B et D, mais, puisque ces quatre régions sont séparées les unes des autres par le bras du fleuve, le voyageur a dû franchir trois ponts; de même, tout parcours dans lequel on traverse quatre ponts sera désigné par cinq lettres. En général, si le voyageur traverse n ponts, la notation de son parcours contiendra n + 1 lettres. Ainsi, {25} dans le problème des sept ponts de Kœnigsberg, tout chemin possible doit être désigné par huit lettres.
6° On observera que, dans cette notation, il n’est pas tenu compte de la désignation des ponts par lesquels le passage s’effectue; il est évident, en effet, que les ponts qui réunissent les mêmes régions peuvent être, dans chaque parcours, remplacés les uns par les autres. Par conséquent, dans le problème des sept ponts, tout parcours est représenté par huit lettres; mais, de plus, ces huit lettres doivent être disposées de telle sorte que la succession immédiate des lettres A et B, dans l’ordre AB ou BA, se présente deux fois, puisqu’il y a deux ponts qui réunissent les rives des régions A et B; de même, le voisinage des lettres A et C doit aussi apparaître deux fois; pour la même raison, il est nécessaire que les lettres B et D, ou C et D soient voisines une seule fois.
7° Le problème particulier se réduit donc à former avec les quatre lettres A, B, C, D une série de huit lettres, dans laquelle tous ces voisinages apparaissent autant de fois qu’il a été indiqué; mais, avant de chercher à effectuer une telle disposition, il est bon de se demander si celle-ci est réalisable. En effet, si l’on démontrait, et c’est ce qui a lieu ici, qu’un tel assemblage de lettres est impossible, il serait inutile de continuer. Aussi ai-je trouvé une règle qui donne, pour tous les cas, la condition indispensable pour que le problème des ponts et des îles ne soit pas impossible.
8° Pour cela, je considère uniquement la région A, dont la rive est réunie a celle des autres régions par un nombre quelconque de ponts a, b, c, d, e, … En commençant par le pont a, j’observe que si le voyageur traverse ce pont, ou bien le voya-{26}geur se trouvait en A avant le passage, ou s’y trouvera après; par conséquent, en franchissant le pont a dans un sens ou dans l’autre, la lettre A paraîtra une seule fois dans la notation. Supposons maintenant que trois ponts a, b, c conduisent dans la région A; si le voyageur traverse les trois ponts, la lettre A apparaîtra deux fois dans la notation, soit qu’au début le voyageur parte de cette région ou d’une autre quelconque. De même, si cinq ponts conduisent en A, la lettre A sera comprise trois fois dans la notation du passage à travers tous ces ponts. En général, si le nombre des ponts qui aboutissent à la rive de la région A est impair (une telle région sera appelée région impaire), la lettre A apparaîtra, dans la notation du passage complet, un nombre de fois égal a la moitié du nombre des ponts augmenté d’une unité. En d’autres termes, si le nombre des ponts est 2n + 1, le nombre d’apparitions de A sera la moitié de 2n + 2 ou n + 1.
9° Dans le cas du problème de Kœnigsberg, cinq ponts aboutissent à la région A, et trois ponts a chacune des régions B, C, D; donc, dans la notation du parcours complet, la lettre A doit apparaître trois fois, et chacune des lettres B, C, D doit être écrite deux fois; par conséquent cette notation devrait renfermer neuf lettres, et non huit, ainsi que nous l’avions trouvé par d’autres considérations. Ainsi le problème de franchir une seule fois tous les ponts de Kœnigsberg n’est pas possible.
10° On appliquera exactement le même raisonnement pour tous les cas dans lesquels le nombre des ponts qui aboutissent aux différentes régions est toujours impair; on pourra déterminer {27} des cas d’impossibilité du parcours. En effet, s’il arrive que le nombre total des apparitions de toutes les lettres n’égale pas le nombre de tous les ponts augmenté de l’unité, le problème est alors impossible. On observera que la règle donnée pour obtenir le nombre des répétitions de la lettre A par le nombre impair des ponts de la région s’applique toujours, soit que tous les ponts issus de la rive A aboutissent à une seule région B, soit qu’ils aboutissent à un nombre quelconque de régions.
11° Mais, lorsque le nombre des ponts issus de A est pair, on doit considérer deux cas, suivant que le voyageur est parti de A ou d’une autre région. En effet, si deux ponts conduisent en A, et si le voyageur est parti de A, alors la lettre A doit être répétée deux fois: une première fois pour le départ par l’un des ponts, et une deuxième fois pour le retour par l’autre pont; mais si le voyageur a commencé ses pérégrinations par une autre région, la lettre A ne se trouvera écrite qu’une seule fois et désignera tout aussi bien, ainsi qu’il est convenu, l’arrivée en A par l’un des ponts et le départ par 1‘autre.
12° Supposons que quatre ponts conduisent dans la région A, et que le voyageur parte de celle-ci; alors la notation du parcours contiendra trois fois la lettre A s’il passe une fois, et une seule, sur chacun de ces ponts; mais s’il est parti d’une autre région, la lettre A ne sera répétée que deux fois. De même, lorsque six ponts aboutissent à la région A, la notation du parcours renfermera quatre fois ou trois fois la lettre A, suivant que le départ s’est effectué de la région A ou d’une autre. En général, lorsque le nombre des ponts d’une rive est pair (région paire), la notation correspondante renferme la lettre de cette région un nombre de fois égal a la moitié du nombre des ponts, si le départ s’est établi {28} d’une autre région, et à ce nombre augmenté de l’unité, si le commencement du voyage a eu lieu dans cette région.
13° Mais il est évident que, dans le parcours complet, on ne peut partir que d’une seule région; par conséquent je prendrai toujours pour le nombre des répétitions d’une lettre la moitié du nombre des ponts pour une région paire, et la moitié du nombre des ponts augmenté d’une unité, si la région est impaire. Nous aurons alors deux cas à considérer, suivant que le départ s’effectue d’une région impaire ou d’une région paire.
Dans le premier cas, le problème sera impossible si le nombre total des répétitions des lettres ne surpasse pas d’une unité le nombre total des ponts. Dans le cas de départ d’une région paire, le problème sera impossible, si le nombre total des répétitions des lettres n’égale pas le nombre des ponts; car, en commençant par une région paire, on devra augmenter d’une unité pour cette région, et pour celle-là seulement, le nombre des répétitions de la lettre correspondante.
14Original: 4 (misprint)° Considérons donc une disposition quelconque des ponts et des îles d’un fleuve. Pour savoir si le parcours complet de tous les ponts n’est pas impossible à priori, on opère de la manière suivante: 1° On désigne chacune des régions séparées les unes des autres par les lettres A, B, C, D; 2° on prend le nombre de tous les ponts, et on le place en tête du tableau de calcul que nous allons indiquer; 3° on écrit dans une colonne verticale chacune des lettres A, B, C, D, et dans une seconde colonne, le nombre des ponts qui aboutissent à ces différentes régions; 4° on {29} marque d’un astérisque les régions paires, c’est-à-dire celles auxquelles aboutissent des ponts en nombre pair; 5° on écrit dans une troisième colonne verticale les moitiés des nombres pairs, et les moitiés des nombres impairs, augmentés d’une unité, de la colonne précédente; 6° on fait la somme de tous les nombres de cette dernière colonne. Lorsque cette somme est égale au nombre de tous les ponts ou lui est supérieure d’une unité, le passage complet peut être effectué, sinon le problème est impossible. Mais il faut observer que, dans le premier cas, le départ doit commencer par une région paire, marquée d’un astérisque; dans le second cas, le départ doit s’effectuer d’une région non marquée d’astérisque, ou impaire. Ainsi l’on a, pour le leThus in the original problème de Kœnigsberg:
| Nombre des ponts: 7. | ||
| A | 5 | 3 |
| B | 3 | 2 |
| C | 3 | 2 |
| D | 3 | 2 |
| Total | 9 |
Comme le total est plus grand que 8 ou 7 + 1, le problème est impossible.
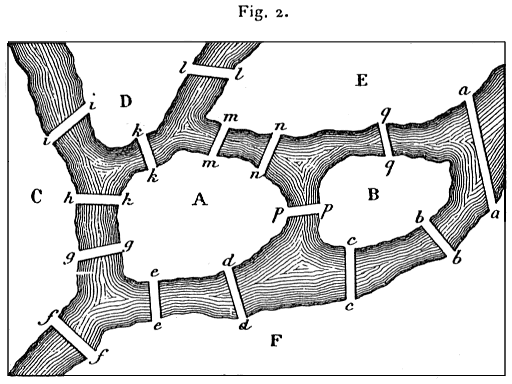
15° Considérons la disposition formée par deux îles A et B, réunies entre elles et aux rives d’un fleuve par quinze ponts, ainsi que l’indique la fig. 2. On demande si l’on peut voyager de manière à passer sur tous les ponts, sans jamais repasser {30} sur l’un deuxRead: d’eux ?. D’abord, je désigne les six régions par les lettres A, B, C, D, E, F; puis je construis le tableau d’après les explications données ci-dessus:
| Nombre des ponts: 15. | ||
| A* | 8 | 4 |
| B* | 4 | 2 |
| C* | 4 | 2 |
| D | 3 | 2 |
| E | 5 | 3 |
| F* | 6 | 3 |
| Total | 16 |
Dans cet exemple, le problème est possible, pourvu que l’on {31} parte de la région D, et alors on arrive à la région E, ou inversement; le parcours pourra s’effectuer ainsi:
EaFbBcFdAeFfCgAhCiDkAmEnApBqElD,
ou dans l’ordre inverse; dans cette notation, nous avons intercalé entre les lettres majuscules, qui indiquent les régions, les lettres minuscules qui désignent les quinze ponts.
16° En dehors de la méthode précédente, pour juger de l’impossibilité, nous indiquerons un moyen plus simple et plus expéditif. Nous observerons d’abord que la somme des nombres de la seconde colonne verticale du tableau est exactement égale au double du nombre des ponts; cela tient à ce que nous avons compté chaque pont deux fois, puisque par chacune de ses extrémités il aboutit à deux régions distinctes.
17° Il résulte évidemment de cette remarque, que la somme des nombres renfermés dans la seconde colonne verticale est un nombre pair, puisque sa moitié représente le nombre des ponts.
Par conséquent, il n’est pas possible que le nombre des régions impaires soit un, trois, cinq, etc.; ainsi dans tous les tableaux de calcul, la seconde colonne renferme toujours un nombre pair de nombres impairs; en d’autres termes, le nombre des régions impaires est nécessairement zéro ou un nombre pair. C’est, en particulier, ce que nous avons trouvé pour le problème de Kœnigsberg, et aussi pour le problème du n° 15.
18° Il ressort de ces considérations que le problème n’est pas impossible si toutes les régions sont paires. Alors tous les nombres de la seconde colonne verticale sont pairs, et le total des {32}
nombres de la troisième colonne est égal au nombre des ponts; et l’on verra que le problème est toujours possible en prenant pour point de départ une région quelconque.
Ainsi, dans l’exemple de Kœnigsberg, on pourrait franchir tous les ponts par deux fois; par exemple:
a b a b c d c d e f f g g e.
En effet, chaque pont est dédoublé, et toutes les régions deviennent paires (1).
(1) Ce raisonnement s’applique évidemment à une distribution quelconque des ponts et des îles dans les bras d’un fleuve, à la condition de passer deux fois sur chaque pont.
19° Supposons encore qu’il y ait deux régions impaires, toutes les autres étant paires; dans ce cas, la somme des nombres de la troisième colonne surpasse d’une unité le nombre des ponts; on s’assurera encore que le problème est possible, à la condition de prendre pour point de départ ou d’arrivée l’une ou l’autre des deux régions impaires. On voit encore que si le nombre des régions impaires était de quatre, six, huit, la somme des nombres de la troisième colonne surpasserait de deux, trois, quatre unités le nombre total des ponts; par conséquent le problème serait impossible.
20° En résumé, étant donnée une disposition quelconque, il sera facile de savoir s’il est possible de franchir, une seule fois, tous les ponts. Le problème est impossible, lorsqu’il y a plus de deux régions impaires; il est possible: 1° lorsque toutes les régions sont paires, et alors le point de départ peut se faire arbitrairement d’une région quelconque; 2° lorsqu’il n’y a que deux régions impaires, et alors le parcours commence par l’une de celles-ci et finit par l’autre, ou inversement.
{33} 21° Lorsque l’on a conclu à la possibilité du problème, il reste à résoudre la question de savoir comment on doit diriger sa course; à cet effet, je me sers de la règle suivante: « On supprime par la pensée, autant de fois qu’on le peut, les couples de ponts qui conduisent d’une région dans une autre; de cette manière, le nombre des ponts est considérablement diminué; on cherche ensuite la course à effectuer avec le reste des ponts. Cela fait, on rétablit les ponts supprimés, ce qui devient très facile avec un peu d’attention. Aussi je ne crois pas qu’il soit nécessaire d’en dire davantage sur la loi de formation des parcours. »
Ici se termine le Mémoire d’Euler. Cet illustre géomètre n’a traité pour ainsi dire que la question d’impossibilité. On trouvera dans la Note II, placée a la fin du volume, la théorie de la possibilité, que l’on doit considérer comme la suite du Mémoire qui précède.
Nous ferons maintenant l’application des règles démontrées dans ce Mémoire au problème suivant: Est-il possible de passer successivement sur tous les ponts de Paris sans passer deux fois sur l’un d’eux?
Nous ne comprenons dans ce problème que les ponts jetés sur la Seine, sans tenir compte des canaux. Dans le parcours du fleuve à travers Paris, on ne rencontre que trois îles, à savoir: l’île Saint-Louis, la Cité et l’île des Cygnes. Par conséquent on doit compter cinq régions différentes: les deux rives et les trois îles.
{34} Mais, parmi ces cinq régions, l’île des Cygnes et la Cité sont des régions paires; à la première aboutissent les deux parties du Pont de Grenelle; a la Cité aboutissent dix ponts, savoir : 1° au sud, le pont de l’Archevêché, le pont au Double, le Petit-Pont, le pont Saint-Michel et la partie méridionale du Pont-Neuf; 2° au nord, le pont Saint-Louis, le pont d’Arcole, le pont Notre-Dame, le pont au Change et la partie septentrionale du Pont-Neuf. L’île Saint-Louis est une région impaire à laquelle aboutissent sept ponts : au sud, la partie méridionale du pont Sully, le pont de la Tournelle et le pont Saint-Louis; au nord, la partie septentrionale du pont Sully, le pont Marie et le pont Louis-Philippe; mais il faut ajouter l’Estacade, pont en bois qui aboutit à la rive droite. Quant aux deux rives, il n’est pas nécessaire de connaître le nombre des ponts; il est facile de voir que l’une d’elles est une région impaire et l’autre une région paire. En effet, il a été démontré au n° 17 que le nombre des régions impaires est toujours pair; or, sur les cinq régions, deux sont paires et une impaire; il est donc nécessaire que l’une des rives soit le point de départ d’un nombre impair de ponts.
D’autre part, puisqu’il n’y a que deux régions impaires, le problème proposé est toujours possible. En d’autres termes, un voyageur peut disposer son parcours de telle sorte qu’il puisse passer une fois, et une seule, sur tous les ponts qui aboutissent à la Cité et à l’île Saint-Louis et sur un nombre quelconque de ponts joignant directement les deux rives de la Seine. Mais le promeneur est toujours forcé de prendre l’île Saint-Louis pour point de départ ou d’arrivée.
On observera d’ailleurs que si l’on ne tient pas compte de l’Estacade, le problème devient d’une très grande simplicité. {35}
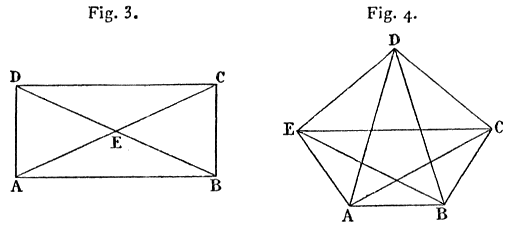
On se propose quelquefois de dessiner, d’un seul trait non doublé, la figure formée par les quatre côtés d’un rectangle et ses deux diagonales. Ce problème est semblable à celui des ponts de Kœnigsberg; soient A, B, C, D les sommets du rectangle, E l’intersection des diagonales. On peut considérer les cinq points A, B, C, D, E comme les centres de cinq régions; quatre d’entre elles, A, B, C, D, sont impaires; donc le problème est impossible. Cependant on pourrait dessiner cette figure en doublant tous les traits.
Ces considérations s’appliquent à la description par un seul trait de toutes les figures de Géométrie formées de lignes droites ou courbes, dans le plan ou dans l’espace. Ainsi on démontrera très facilement que l’on peut décrire d’un seul trait la figure formée par les côtés et toutes les diagonales d’un polygone convexe d’un nombre impair de côtés, et que le problème est impossible pour les polygones d’ordre pair, comme le carré, l’hexagone. De même, on peut décrire d’un seul trait l’ensemble des arêtes de {36} l’octaèdre régulier, tandis qu’on ne peut le faire pour les quatre autres polyèdres réguliers convexes.
Je me suis laissé dire que Mahomet dessinait d’un seul coup, avec la pointe de son cimeterre, sa signature formée de deux croissants opposés, conformément à la fig. 5. En effet, cette figure ne contient que des points d’ordre pair, et peut se décrire d’un seul trait continu.
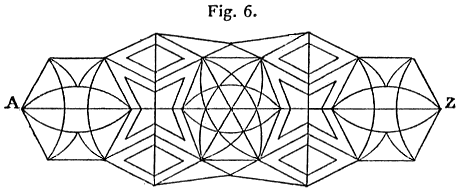
La fig. 6 ne contient que deux points impairs A et Z; par conséquent, on peut la décrire d’un seul trait continu allant de A à Z ou inversement. On peut réaliser un jeu, en dessinant cette figure en grand sur une feuille de carton; on place de petits jetons sur le milieu de toutes les lignes qui joignent deux points {37} voisins; il s’agit alors de déterminer le parcours à suivre pour enlever tous les jetons successivement. Cette figure est extraite de l’opuscule ayant pour titre: Vorstudien zur Topologie, par Johann Benedict Listing; cet ouvrage curieux m’a été gracieusement communiqué par M. Moritz Cantor, professeur à l’Université de Heidelberg.
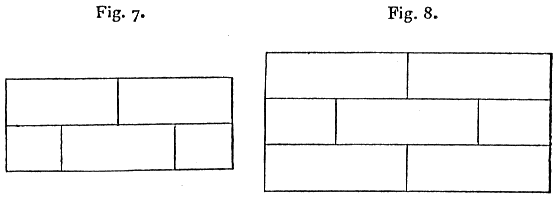
La fig. 7 contient huit points impairs et ne peut être décrite en moins de quatre traits continus; ce théorème a été énoncé par Clausen, dans le n° 494 des Astronomische Nachrichten. La fig. 8 représente un fragment de mur en maçonnerie; elle contient douze points impairs, et ne peut être décrite en moins de six traits continus.
De même, la figure qui représente l’échiquier ordinaire de soixante-quatre cases renferme vingt-huit points impairs, et ne peut être décrite en moins de quatorze traits; la figure du damier de cent cases nécessite la succession de dix-huit traits continus.
Si l’on divise les côtés d’un triangle en n parties égales, et si l’on joint les points de division correspondants par des lignes parallèles aux côtés, on obtient une figure qui ne contient que {38} des points d’ordre pair, et que l’on peut décrire d’un seul trait, etc.
On ramène encore au problème des ponts de Kœnigsberg celui du voyage d’un contrebandier qui se propose de traverser successivement toutes les frontières respectives des divers pays d’un continent, et de ne les traverser qu’une seule fois. Il est évident que les divers pays et leurs frontières correspondent exactement aux régions et aux bras du fleuve sur lesquels serait jeté un seul pont, pour chaque frontière commune a deux pays. Ainsi, puisque la Suède, l’Espagne et le Danemark ont des frontières en nombre impair [7], il est impossible de traverser, une seule fois seulement, toutes les frontières des différents pays de l’Europe.
Il y a encore lieu de considérer le problème géométrique corrélatif pour les figures du plan et de l’espace. Ainsi, par un mouvement continu sur la surface, il est possible de traverser une seule fois toutes les arêtes du cube, mais non pas les arêtes des autres polygones réguliers convexes.