It is proved below that the conjecture is true, but the generalization to all real r>1 is false.
At first, try generalizing to any r>1 and replace xn (n>0) by any function ƒ(x) such that
- ƒ(x) is defined and increasing for x≥0;
- ƒ(x) has a left-hand derivative at r.
Generalize u and w to:
| u(k)=⌊kƒ(r)⌋, w(k)=⌊kƒ(⌊kr⌋/k)⌋, |
and write Δ(k) for u(k)−w(k).
Although the conjecture in this more general form turns out to be false (see below) the discussion will throw light on the proof of the original conjecture.
Define ξk={kr}, where {⋅} denotes the fractional part. Define gk by
| gk= | [ƒ(r)−ƒ(r−ξk/k)]/(ξk/k) | if ξk>0 |
| ƒ′(r) | if ξk=0. |
Then gk→ƒ′(r) as k→∞. We have
| ƒ(⌊kr⌋/k)=ƒ((kr−ξk)/k)=ƒ(r−ξk/k)=ƒ(r)−gk(ξk/k), |
and hence
| u(k)=⌊kƒ(r)⌋, w(k)=⌊kƒ(r)−gkξk⌋. |
Define ηk={kƒ(r)}. By hypothesis gk>0 and hence
| Δ(k)=0 iff | 0 | <gkξk≤ηk |
| Δ(k)=1 iff | ηk | <gkξk≤ηk+1 |
| Δ(k)=2 iff | ηk+1 | <gkξk≤ηk+2 |
| Δ(k)=3 iff | ηk+2 | <gkξk≤ηk+3 |
etc. In general, Δ(k)=⌈gkξk−ηk⌉. For m=0,1,…,⌈gk⌉ let R(k,m) be the set of (ξ,η) such that
| 0≤ξ<1, 0≤η<1, ⌈gkξ−η⌉=m. | (1) |
Then Δ(k)=m iff ({kr},{kƒ(r)})∈R(k,m). Figures 1a, 1b show examples of the regions R(k,m), with the values of m, for gk>1 and gk<1 respectively.
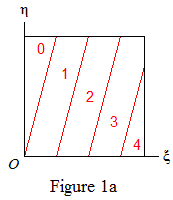
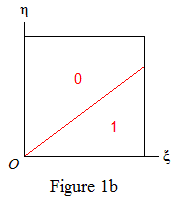
Recalling that gk→ƒ′(r)=g, say, define R(∞,m) as in (1) with gk changed to g. The basic idea is:
Lemma 1. Suppose R(∞,m) has a subset S such that
| (i) | S lies at a strictly positive distance from the bounding lines of R(∞,m); |
| (ii) | S contains infinitely many of the points ({kr},{kƒ(r)}). |
Then Δ(k)=m for infinitely many k.
Proof. Since gk→g, (i) implies that S⊂R(k,m) for all sufficiently large k. Hence for infinitely many k we have ({kr},{kƒ(r)})∈R(k,m), that is, Δ(k)=m. ■
Setting s=ƒ(r), we are therefore led to look at the distribution of ({kr},{ks}) within the unit square, where r and s are fixed real numbers and k runs through the positive integers.
What complicates the proof, and causes the generalized conjecture to fail, is the possibility that r and s are linearly dependent over the integers. i.e. that there exists a relation
| ar−bs+c=0 (a,b,c)≠(0,0,0) | (2) |
for some integers a,b,c. If no such relation exists (which implies that r and s are both irrational) then the ({kr},{ks}) are uniformly distributed in the unit square (J.W.S. Cassels, An Introduction to Diophantine Approximation, Cambridge University Press, 1957, p. 60).
If r and s are both rational then clearly the ({kr},{ks}) consist of a finite set of points, which occur equally often. The remaining case requires more work.
Lemma 2. Suppose that r,s are not both rational and are linearly dependent over the integers, i.e. there exist integers a,b,c satisfying (2). Assume w.l.o.g. that a,b,c have no common factor. Then the points ({kr},{ks}) are uniformly distributed on a set of parallel line segments, namely the set of (ξ,η) such that
| 0≤ξ<1, 0≤η<1, aξ−bη=h, | (3) |
where h is an integer and −b+1≤h≤a−1.
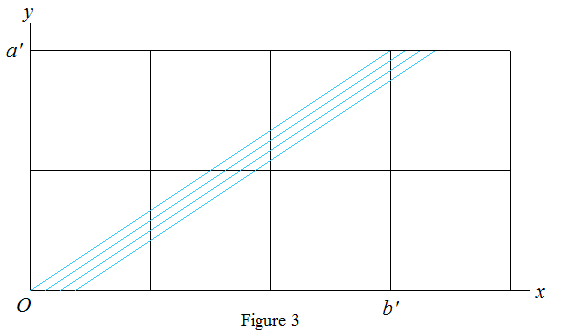
Remark. Figures 2a, 2b illustrate the cases a=8, b=12 and a=8, b=−12 respectively. The points ({kr},{ks}) are uniformly distributed on the set of blue lines.
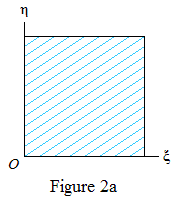
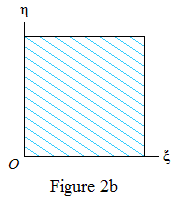
Proof. Assume w.l.o.g. that b is irrational. Then a≠0 and w.l.o.g. a>0. Replacing s by −s if necessary we may assume b≥0. Define d=HCF(a,b); then HCF(c,d)=1. Define a′=a/d, b′=b/d. We first replace the parallel line segments (3) by another set
| 0≤y<a′, ax−by=l | (4) |
where l is an integer and 0≤l<d. See Figure 3, drawn with the same parameters as Figure 2a, i.e. a=8, b=12, whence d=4, a′=2, b′=3.
Figures 2a and 3 show that the original line segments (3) are the line segments (4) taken modulo the unit square. To prove this formally, define a map μ from the set of line segments (3) to the set of line segments (4) as follows. Given (ξ,η) in (3), there are unique integers l,m such that h=md+l,0≤l<d. Since a′,b′ are coprime there are then unique integers p,q such that m=−a′p+b′q,0≤q<a′. Define μ(ξ,η)=(x,y) where x=ξ+p, y=η+q. We check that 0≤y<a′ and
| ax−by=aξ−bη+ap−bq=h+(a′p−b′q)d=md+l−md=l, |
so that (x,y) does lie on one of the segments (4). We show that μ is a bijection.
If (x,y)=μ(ξ,η) then (ξ,η)=({x},{y}). Hence μ is (1–1).
Given any (x,y) satisfying (4) define ξ={x} and η={y}. Clearly aξ−bη=h where h is an integer, and −b+1≤h≤a+1 since ξ,η∈[0,1], so (ξ,η) satisfies (3). Define p=x−ξ, q=y−η, m=−a′p+b′q. Then
| h=aξ−bη=a(x−p)−b(y−q)=l−ap+bq=md+l. |
Since 0≤l<d it follows from the definition of μ that (x,y)=μ(ξ,η). Hence μ is onto.
For positive integer k define (ξk,ηk)=({kr},{ks}) and (xk,yk)=μ(ξk,ηk). To show that (ξk,ηk) is uniformly ditributed on the set (3), it suffices to show that (xk,yk) is uniformly distributed on (4). In the following, hk etc. are the values of h etc. derived from (ξk,ηk).
Since d divides a we have axk≡aξk=a{kr}≡akr (mod d), and similarly byk≡bks (mod d). Hence
| lk=axk−byk≡akr−bks=−kc (mod d) |
Recall c and d are coprime; hence as k runs through the positive integers, lk cycles through the values 0,1,…,d−1 in some order, with ld=0. So (xk,yk) visits each line segment in (4) at intervals of d. Given k, define integers uk, vk by
| uk={(k+d)r}−{kr}−{dr}, vk={(k+d)s}−{ks}−{ds} |
We have a{kr}−b{ks}=hk=mkd+lk and similarly for the suffixes k+d, d. Since lk+d=lk and ld=0 this implies
| auk−bvk=(mk+d−mk−md)d. |
Substituting mk=−a′pk+b′qk etc. and dividing by d gives
| a′(uk+pk+d−pk−pd)=b′(vk+qk+d−qk−qd). |
Since a′ and b′ are coprime, a′ divides (vk+qk+d−qk−qd). On any line segment in (4), the change in y on successive visits of (xk,yk) is
| yk+d−yk | ={(k+d)s}+qk+d−{ks}−qk |
| ={ds}+vk+qk+d−qk | |
| ≡{ds}+qd (mod a′). |
Hence yk increases by a constant irrational amount (mod a′) at each visit. Hence the distribution of (xk,yk) along each line segment is uniform. ■
Counterexample to the generalization
Before discussing the case r=Φ=(1+√5)/2, it may be helpful to see why the conjecture is false for some values of r. Consider the case r=√2, ƒ(x)=x3. Here s=ƒ(r)=2√2, so r and ƒ(r) are dependent over the integers: equation (2) holds with a=2, b=1, c=0. We have g=ƒ′(r)=6. Figure 4a shows (red) the regions R(k,m) for a typical k, and Figure 4b the regions R(∞,m). The points ({kr},{kƒ(r)}) lie on the blue lines.
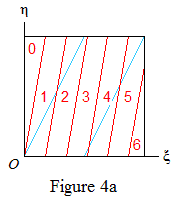
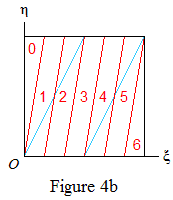
It can be seen that the only possible values of Δ(k) are 1, 2, 3, 4, 5 and that each of 1, 2, 4, 5 occurs infinitely often. It will be shown that Δ(k)=3 only if k=2, so that the generalized conjecture fails in this case.
In Figure 4a the left-hand boundary of R(k,3) meets the top of the square at (3/gk,1). Since ƒ is here a convex function, gk<g=6 for all k. Hence 3/gk>1/2, and the left-hand blue line does not intersect R(k,3). So if Δ(k)=3 then ({kr},{kƒ(r)}) lies on the right-hand blue line: say
| kr=k√2=h+1/2+ε |
| kƒ(r)=k2√2=2h+1+2ε |
where h is an integer and 0<ε<1/2.
Clearly u(k)=⌊kƒ(r)⌋=2h+1 and w(k)=⌊k(⌊kr⌋/k)3⌋=⌊h3/k2⌋, so that Δ(k)=3 iff
| 2h−2≤h3/k2<2h−1. | (8) |
Define t=8k2−(2h+1)2. Then t>0 and t≡−1 (mod 8), so t≥7. A routine calculation shows that
| 4[(2h−2)k2−h3]=t(h−1)−3h−1≥7(h−1)−3h−1=4h−8, |
so the first inequality in (8) implies 4h−8≤0. Since h=⌊k√2⌋, the only possibilities are (h,k)=(1,1) or (2,2); and only the second of these satisifies the second inequality in (8).
Remark. It’s interesting to compare this with what happens if, keeping ƒ(x)=x3, we take r=√3. Although the proportion of k such that Δ(k)=3 tends to 0, there are now infinitely many such k. See the appendix for details.
Proof of the conjecture when r=(1+√5)/2
Write Φ for (1+√5)/2. We now have ƒ(x)=xn where n>0. To cope with the possibility that Φ and Φn are linearly dependent over the integers, we need, in addition to Lemma 2:
Lemma 3. If Φ and Φn are linearly dependent over the integers, and n≠1, then the gradient nΦn−1 is irrational.
Proof. Suppose aΦ−bΦn+c=0 where a,b,c are integers not all 0, and suppose, for a contradiction, that nΦn−1 is rational.
If c=0 then Φn−1=a/b is rational, hence n is rational; say n−1=p/q, where p,q are integers and by hypothesis p≠0. Then Φ p=(a/b)q is rational. This is a contradiction, since Φ p is irrational for integer p≠0. (Note here the difference between r=Φ and the counterexample r=√2.)
If c≠0, then a+cΦ−1 is irrational and algebraic. Since n(a+cΦ−1)=bnΦn−1 is rational, n is also irrational and algebraic. Then since Φ is algebraic, Φn is transcendental by the Gelfond–Schneider theorem. But Φn is the product of the algebraic numbers n−1, nΦn−1, Φ: contradiction. ■
The cases n=1, n>1, n<1 will now be considered separately.
Case n = 1. This is trivial: Δ(k)=0 for all k, so the result holds vacuously with M=0.
Case n > 1. If Φ and Φn are linearly independent over the integers, then the points ({kΦ},{kΦn}) are distributed uniformly in the unit square, so every value of Δ(k) from 0 to ⌈g⌉=⌈nΦn−1⌉ occurs infinitely often. Further, as k→∞, the proportion of k for which Δ(k)=m tends to the area of R(∞,m).
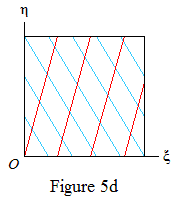
Figure 5 shows some examples of what happens if Φ and Φn are linearly dependent. As before, the red lines mark the regions R(∞,m) and the points ({kΦ},{kΦn}) lie on the blue lines. The red lines have gradient g=nΦn−1, which is irrational by Lemma 3; hence a red line and a blue line never meet a side of the square at the same point (other than the origin).
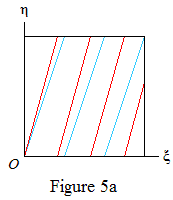
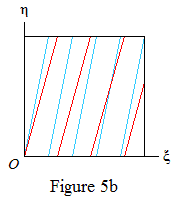
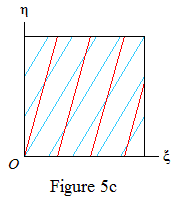
If a and b have the same sign (Figures 5a, 5b, 5c), consider tracing the blue line upwards from (0, 0). It starts in the region R(∞,0) or R(∞,1). If it hits the top of the square in the region R(∞,m) it wraps round to a point in R(∞,m+1). Hence, each R(∞,m) for m=1,…,⌈g⌉−1 contains a non-zero segment of blue line. In Lemma 1 we can take S to be (say) the middle third of this segment and conclude that each value Δ(k)=1,…,⌈g⌉−1 occurs for infinitely many k.
If R(∞,⌈g⌉) is cut by a blue line, then Δ(k)=⌈g⌉ also occurs for infinitely many k. Else note that xn is a convex function for n>1, so that for all k we have gk≤g and hence R(k,⌈g⌉)⊆R(∞,⌈g⌉). So no R(k,⌈g⌉) is cut by a blue line, and Δ(k)=⌈g⌉ does not occur at all. The conjecture holds in either case, with M=⌈g⌉ or ⌈g⌉−1 respectively.
(We have not discussed how often Δ(k)=0 occurs, but the conjecture as stated does not require this.)
If a and b have opposite signs (Figure 5d) the argument is similar, but now the values Δ(k)=0,⌈g⌉ necessarily occur. The conjecture holds with M=⌈g⌉.
Case n < 1. Here g=ƒ′(Φ)=nΦn−1<1. Further, since ƒ(Φ)<Φ and ƒ is a concave function, gk<1 for each k. Hence the only possible values of Δ(k) are 0 and 1. We need to show that the value 1 occurs infinitely often or not at all.
If Φ and Φn are linearly independent over the integers, then the points ({kΦ},{kΦn}) are uniformly distributed in the unit square and each value Δ(k)=0,1 occurs infinitely often. Further, as k→∞, the proportion of k for which Δ(k)=1 tends to the area of R(∞,1), i.e. nΦn−1/2.
Suppose Φ and Φn are linearly dependent, i.e.
| aΦ−bΦn+c=0 (a,b,c)≠(0,0,0), | (9) |
where b≠0 (since Φ is irrational) and w.l.o.g. a≥0. The value Δ(k)=1 occurs infinitely often if R(∞,1) (the triangle below the red line in Figures 6 and 7) is cut by a blue line.
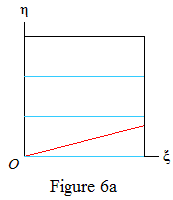
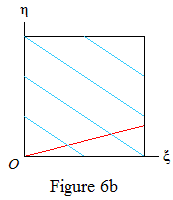
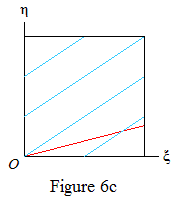
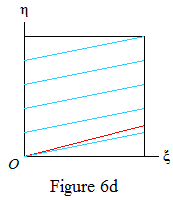
Thus Δ(k)=1 occurs infinitely often if a=0 (Figure 6a), or b<0 (6b). Suppose now that a,b>0. Then Δ(k)=1 occurs infinitely often if a>1 (6c), or a=1 and g>1/b (6d). Since g≠1/b by Lemma 3, it remains to deal with the case a=1, g<1/b (Figure 7).
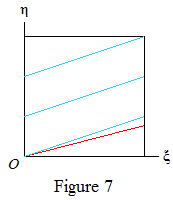
Here Δ(k)=0 for all large enough k. We need to show that Δ(k)=1 never occurs at all. The proof is more complicated than for n>1, since xn is now a concave function and the relation R(k,⌈g⌉)⊆R(∞,⌈g⌉) used for n>1 is reversed.
Lemma 4. For real t>0 define λ(t)=(1+t−1)ln(1+t), and define λ(0) by continuity. Then λ(t) is an increasing function of t with λ(0)=1.
Proof. For small t>0 we have λ(t)=1+t/(1×2)−t2/(2×3)+t3/(3×4)−…, so λ(0)=1. A routine calculation shows that λ′(t)>0 is equivalent to the well-known inequality exp(t)>1+t. ■
With a=1, (9) gives Φ−bΦn+c=0. Since 0<n<1, so 1<Φn<Φ. If b=1 this gives 1−Φ<c<0, a contradiction since c is an integer. Hence b≥2. Next, b−c<bΦn−c=Φ, hence b−c≤1 (since b,c are integers), hence c≥b−1. We show that, for a given b, the condition nΦn−1=g<1/b is satisfied only when c=b−1. Since n, and therefore nΦn−1, increases with c, it suffices to show that nΦn−1>1/b when c=b. In this case
| Φn−1=1/b+1/Φ, n=ln(1+Φ/b)/lnΦ, |
so we have to prove (1+b/Φ)ln(1+Φ/b)>lnΦ. Since lnΦ<1, this follows from Lemma 4 with t=Φ/b.
Conversely, suppose c=b−1. To show that nΦn−1<1/b, note that
| Φn−1=(Φ−1+b)/bΦ, n=ln(1+(Φ−1)/b)/lnΦ. |
Set t=(Φ−1)/b. Another short calculation shows that nΦn−1<1/b is equivalent to λ(t)<ΦlnΦ/(Φ−1) = 1.2598…. Since t≤(Φ−1)/2 and λ((Φ−1)/2)=1.1406…, the result follows from Lemma 4.
Assuming then that Φ−bΦn+b−1=0, with 0<n<1 and b≥2, we have to show the Δ(k) are all 0. For k≥2 we have 1/k<Φ−1 and therefore, since ƒ(x)=xn is a concave function when 0<n<1,
| gk<[ƒ(Φ)−ƒ(Φ−1/k)]/(1/k)<[ƒ(Φ)−ƒ(1)]/(Φ−1)=1/b. |
Hence R(k,1) lies below all the blue lines in Figure 7, and Δ(k)=0.
For k=1 we have u(1)=⌊Φn⌋=1 and w(1)=⌊⌊Φn⌋⌋=1, so Δ(1)=0. This completes the proof.
Appendix: the case ƒ(x)=x3, r=√3
This looks at first very similar to the counterexample with the same ƒ and r=√2. The possible values for Δ(k) are 1,…,8. The proportion of k for which Δ(k)=3 or 6 tends to 0 as k→∞. If Δ(k)=3 then, similarly to the case r=√2, we have
| kr=k√3=h+1/3+ε |
| kƒ(r)=k3√3=3h+1+3ε |
where h is an integer and 0<ε<1/3.
We have u(k)=⌊kƒ(r)⌋=3h+1 and w(k)=⌊k(⌊kr⌋/k)3⌋=⌊h3/k2⌋, so that Δ(k)=3 iff
| 3h−2≤h3/k2<3h−1. | (10) |
Define t=27k2−(3h+1)2. Then t>0 and t≡2 (mod 3). A routine calculation shows that the left-hand inequality in (10) is equivalent to
| 3(t−3)h≤2(t−1). |
If t≠2 then t≥5, hence h≤1, hence k√3<5/3, a contradiction. Hence if Δ(k)=3 then t=2.
Conversely, given positive integers h,k such that 27k2−(3h+1)2=2, it is easy to verify that ⌊k√3⌋=h, ⌊k3√3⌋=3h+1, and ⌊h3/k2⌋=3h−2, whence Δ(k)=3. To find such h,k consider the diophantine equation
| 27k2−l2=2. |
This has the obvious solution (k1,l1)=(1,5). From this and the solution to the Pell equation p2−27q2=1, viz. (p,q)=(26,5), one can generate all solutions in the usual way, by setting
| (ki+1,li+1)=(pki+qli,27qki+pli)=(26ki+5li,135ki+26li). |
Clearly li+1≡−li (mod 3), with l1≡−1, so when i is even li has the form 3h+1 and Δ(ki)=3. Hence there are infinitely many k such that Δ(k)=3, though they are scarce: the first three are 51, 137801, 372338251.
The case Δ(k)=6 is probably similar, but hasn’t yet been analyzed.
Michael Behrend 18 June 2012