Probability moments for ellipse and rectangle

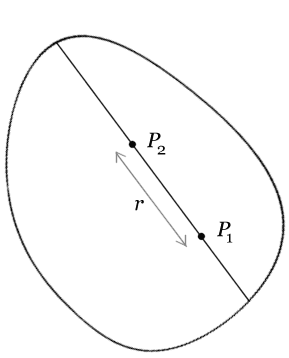
Let K be a finite plane convex region. In working out the expected number of alignments in a random set of points, with independent uniform distributions in K, we need the moments of the p.d.f. for |P₁P₂|, the distance between two points P₁ and P₂ with independent uniform distributions in K. Denote by M_n the nth moment, i.e. the mean value of |P₁P₂|ⁿ.

With a strip criterion, the expected number of r-point alignments (r≥3) typically depends on M_r−2, so that all positive moments are needed. With an angle criterion, the expected number of r-point alignments typically depends on M_2r−4, so that only even moments are needed. In the formulae below, the form of M_n differs for odd and even n.

The lists below give the first few values of M_n for K = ellipse and rectangle, with circle and square listed separately for convenience. There is then a description of how the moments can be calculated for these K.

Circle

For a circle with radius a :

M1=  128a 45π

M2=  a2

M3=  2048a3 525π

M4=  5a4 3

M5=  16384a5 2205π

M6=  7a6 2

Ellipse

For an ellipse with semi-major axis a and eccentricity e :

Here K(e) and E(e) are complete elliptic integrals (see below).

M1  =  256a E(e) 45π2 M1  =  128a ( 1−  1 e2−  3 e4−  5 e6−  175 e8−  441 e10−… ) 45π 4 64 256 16384 65536

M2  =  ( 1−  1 e2 ) 2

M3  =  4096a3 ( (4−2e2)E(e)−(1−e2)K(e) ) 1575π2 M3  =  2048a3 ( 1−  3 e2+  9 e4+  5 e6+  105 e8+  189 e10+… ) 525π 4 64 256 16384 65536

M4  =  5a4 ( 1−  e2+  3 e4 ) 3 8

M5  =  32768a3 ( (23−23e2+8e4)E(e)−4(1−e2)(2−e2)K(e) ) 33075π2 M5  =  16384a5 ( 1−  5 e2+  45 e4−  25 e6−  175 e8−  189 e10−… ) 2205π 4 64 256 16384 65536

M6  =  7a6 ( 1−  3 e2+  9 e4−  5 e6 ) 2 2 8 16

Square

For a square with side a :

M1=  a ( 2+√2+5ln(√2+1) ) 15

M2=  a2 3

M3=  a3 ( 8+17√2+21ln(√2+1) ) 210

M4=  17a4 90

M5=  a5 ( 16+73√2+45ln(√2+1) ) 1008

M6=  29a6 210

Rectangle

For a rectangle with sides a and b :

Let d=√(a²+b²), and let

Ln=  an+1 ln ( d+b ) +  bn+1 ln ( d+a ) b a a b

Then

M1=  1 ( 10d−  2(d 5−a5−b5)  +5L1 ) 30 a2b2

M2=  1 d 2 6

M3=  1 ( 49d 3−  8(d 7−a7−b7)  +21L3 ) 420 a2b2

M4=  1 ( 6a4+5a2b2+6b4 ) 90

M5=  1 ( 3d (41a4+52a2b2+41b4)−  16(d 9−a9−b9)  +45L5 ) 2016 a2b2

M6=  1 ( 15a6+14a4b2+14a2b4+15a6 ) 420

A theorem of Santaló

A theorem given by Santaló [Ref. 1] is useful in calculating the moments.

Let P₁P₂=r. Santaló defines

Jn=  ∫   rndP1dP2 . P1 ,P2∈K

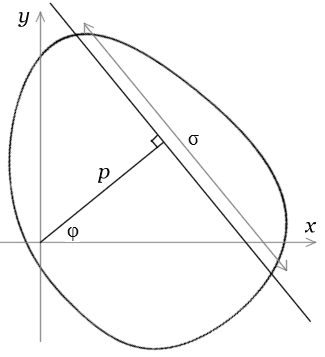
Let G be a variable line defined by coordinates (p,φ) (Fig. 1b), and if G meets K let σ be the length of the chord so defined. Santaló defines

In=  ∫   σndG , G∩K≠∅

which we may write as

In=  ∫ ∞  ∫ 2π σndpdφ , p=0 φ=0

taking σ=0 if G does not meet K. Santaló proves that

Jn=  2 In+3 . (n+2)(n+3)

Now let |K| be the area of K and let M_n be the nth moment of the p.d.f. of r. Clearly

Mn=  Jn |K|2

and consequently

Mn=  2   In+3  . (n+2)(n+3) |K|2

It may be easier to evaluate I_n+3 and apply this formula, than to evaluate M_n directly.

Moments for an ellipse

We evaluate M_n for an ellipse from Santaló’s I_n+3, as above.

Let the equation of the ellipse be x²/a²+y²/b²=1, and let e be the eccentricity, so that b²=a²(1−e²). Setting

q(φ)=a(1−e2sin2φ)1/2 ,

we find by a routine calculation that the line (p,φ) meets the ellipse iff |p|≤q(φ), and then

σ=2abq(φ)−2 (q(φ)2−p2)1/2 .

Putting p = q(φ)sinθ gives

In=  ∫ π/2  ∫ 2π  [2abq(φ)−2]n [q(φ)cosθ]n+1dθdφ = 2nCn+1abn ∫ π/2  (1−e2sin2φ)−(n−1)/2 , θ=0 φ=0 0

where

Cm=  ∫ π/2  cosmθdθ , so that C0=π/2, C1=1, Cm=Cm−2(m−1)/m  (m=2,3,…). 0

Combining, and noting that the integral from 0 to 2π is 4 times the integral from 0 to π/2, we get

Mn=  2n+6Cn+4   bn+1 ∫ π/2  (1−e2sin2φ)−(n+2)/2dφ. (n+2)(n+3) π2a 0

The integral here (call it A_n) can be done for a particular e by numerical integration. Alternatively, it can be solved explicitly as follows. To bring A_n into the form tabulated by Gradshteyn & Ryzhik [Ref. 2], define

θ=π−2φ, c=(1−e2)1/2, ƒ=  1−c  . 1+c

Then

An=  ∫ π/2  (1−e2sin2φ)−(n+2)/2=2n+1(1−c)−(n+2) ∫ π  (1−2ƒcosθ+ƒ2)−(n+2)/2 . 0 0

Case of even n.  Let n=2m. From item 3.616.2 of [Ref. 2],

An=2n+1(1+c)−(n+2)×π(1−ƒ2)−(m+1) ∑ m (m+k)! uk , k=0 k!2(m−k)!

where u=ƒ²/(1−ƒ²)=(1−c)²/4c. Simplifying slightly,

An=π(2c)−(2m+1) ∑ m (m+k)! (1−c)2k(4c)m−k . k=0 k!2(m−k)!

One checks empirically (I have no proof yet) that

∑ m (m+k)! (1−c)2k(4c)m−k=  ∑ m (2k)!   (2m−2k)! c2k=  ∑ m (2k)!m! 4m−k(−e2)k . k=0 k!2(m−k)! k=0 k!2 (m−k)!2 k=0 k!3(m−k)!

For even n=2m we conclude

Mn=  2n+4 ⋅ n+1 ⋅ n−1 ⋅…⋅ 1 an ∑ m (2k)!m! (−e2/4)k , (n+2)(n+4) n+2 n 2 k=0 k!3(m−k)!

where for a circle (e = 0) the sum equals 1.

Case of odd n.  Let n = 2m – 1. From item 3.617 of [Ref. 2],

An=  2n+1   2  Fm ( 2ƒ1/2 )  , (1+c)n+2 (1+ƒ)n+2 1+ƒ

where the functions F_m are defined below. Since (1+c)(1+ƒ)=2 and 2ƒ^1/2(1+ƒ)=e, we have

Mn=  2n+6Cn+4   an  (1−e2)m Fm(e) . (n+2)(n+3) π2

We now define the F_m as in [Ref. 2]. F₀ is the complete elliptic integral of the first kind, given by

F0(e)= K(e)=  ∫ π/2 (1−e2sin2θ)−1/2dθ=  π ( 1+  12 e2+  12⋅32 e4+  12⋅32⋅52 e6+… ) 0 2 22 22⋅42 22⋅42⋅62

and the F_m satisfy the recurrence relation

Fm+1(e)=Fm(e)+  e   dFm(e)  (m=0,1,2,…). 2m+1 de

In our case it is convenient to define G_m(e)=(2/π)(1−e²)^m F_m(e). The recurrence relation for the G_m is

Gm+1(e)=Gm(e)+  1 ( e(1−e2) dGm(e)  −e2Gm(e) )  (m=0,1,2,…). 2m+1 de

If we introduce as in [Ref. 2] the complete elliptic integral of the second kind, given by

E(e)=  ∫ π/2 (1−e2sin2θ)1/2dθ=  π ( 1−  1 e2−  12⋅3 e4−  12⋅32⋅5 e6−… ) 0 2 22 22⋅42 22⋅42⋅62

then the derivatives

dK(e)  =  E(e)  −  K(e)  ,   dE(e)  =  E(e)− K(e)  , de e(1−e2) e de e

combined with the recurrence relation for F_m, lead to

G1(e)=  2 (1−e2) F1(e)=  2 E(e) , π π

G2(e)=  2 (1−e2)2 F2(e)=  2 ( (4−2e2)E(e)−(1−e2)K(e) )  , π 3π

G3(e)=  2 (1−e2)3 F3(e)=  2 ( (23−23e2+8e4)E(e)−4(1−e2)(2−e2)K(e) )  , π 15π

and so on (the working becomes laborious). Alternatively, the recurrence relation for G_m leads to

Gm(e)=1−  1 (2m−1)e2+  1.3 (2m−1)(2m−3)e4−  1⋅3⋅5 (2m−1)(2m−3)(2m−5)e6+… . 22 22⋅42 22⋅42⋅62

For odd n=2m−1 we conclude

Mn=  2n+4 ⋅ n+1 ⋅ n−1  …  2 ⋅ 2 an Gm(e) , (n+2)(n+4) n+2 n 3 π

where for a circle G_m(0) = 1.

It is possible to combine the results for even and odd n into a single formula, but this is less convenient for applications.

Moments for a rectangle

We evaluate M_n for a rectangle from Santaló’s I_n+3, as above.

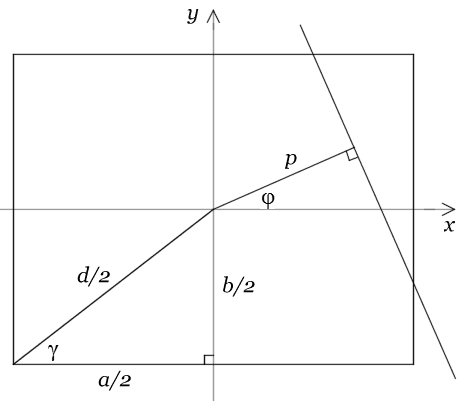
Let the diagonal of the rectangle be d, and let the sides be a=dcosγ, b=dsinγ. It suffices to consider 0≤φ≤π/2.

First suppose 0≤φ≤π/2−γ. Define p₁=(d/2)cos(γ+φ) , p₂=(d/2)cos(γ−φ)S. The chord length σ for the line (p,φ) is given by

σ=bsecφ  if  0≤p≤p1 σ=bsecφ×(p2−p)/(p2−p1)  if  p1≤p≤p2 0  if  p>p2

from which we easily find

∫ ∞ σndp=(d sinγ secφ)n  ( d cos(γ+φ)  +  d sinγ sinφ ) . 0 2 n+1

Similarly, for π/2−γ≤φ≤π/2 we find

∫ ∞ σndp=(d cosγ cosecφ)n  ( −  d cos(γ+φ)  +  d cosγ cosφ ) , 0 2 n+1

which has the same form as the first integral if we put  γ=π/2−γ′,  φ=π/2−φ′.

Integrating over φ=0 to 2π we find for n>0 that

In=2d n+1 sinnγ cosγ ∫ π/2−γ secn−1φdφ−  2 d n+1(sin2γ−sinn+1γ)+ comp, 0 n+1

where “comp” is obtained by putting π/2−γ in place of γ. Recall that if

Sm(θ)=  ∫ θ secmφdφ 0

for 0≤θ≤π/2 and integer m>0, then

S1(θ)=ln(secθ+tanθ), S2(θ)=tanθ, Sm(θ)=  1 tanθ secm−2θ+  m−2 Sm−2(θ) (m=3,4,…). m−1 m−1

Hence if we define

U2=  d ln ( d+b ) , U3=1, Um=  1  +  m−3 ⋅ a2 Um−2 , b a m−2 m−2 d 2

V2=  d ln ( d+a ) , V3=1, Vm=  1  +  m−3 ⋅ b2 Vm−2 , a b m−2 m−2 d 2

then the moments M_n are given by

Mn=  4 ( d n (Un+3+Vn+3) −  d  n+4−a n+4−b n+4 ) . (n+2)(n+3) (n+4)a2b2

For even n this expression reduces to a polynomial in a²,b². Putting n=2m we have

M2m=m! ∑ m a2(m−k) b2k  . k=0 (2k+1) (2m−2k+1) (k+1)! (m−k+1)!

There does not seem to be a similar result for odd n.

References

[1]	Luis A. Santaló, Integral Geometry and Geometric Probability (Vol. 1 of Encyclopedia of Mathematics and its Applications), Addison-Wesley, 1976, pp. 45–49.
[2]	I.S. Gradshteyn & I.M. Ryzhik, Table of Integrals, Series, and Products, 6th edn, Addison-Wesley, 2000, pp. 387–388.