page 29

Appendix 4: Triangular Arrangements of Sites

BF 1975; addendum MB 2014

A. Right-angled triangles

Appendix 4 figure a

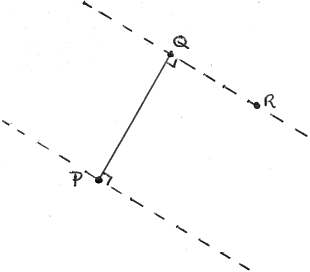
Fix two ley points P and Q. Construct the lines (dotted) through P and Q which are perpendicular to PQ. If any ley point R falls on either dotted line, a right angled triangle PQR results.

The mean number of points R falling on the dotted lines is

2×(n–2)p

(where p is as defined in the Introduction) and so PQ results in, on average, 2(n−2)p right-angled triangles.

There are ⁿC₂ ways of choosing the initial pair of points P and Q. Therefore there are

½×ⁿC₂×2(n–2)p=½n(n–1)(n–2)p

right angled triangles to be found over the whole map, the prefixed factor of ½ being because each triangle is counted twice in summing over the whole map.

Appendix 4 figure b

Thus:

N(Rt.)=	n(n−1)(n−2) p	.
	2

B. Equilateral triangles

Appendix 4 figure c

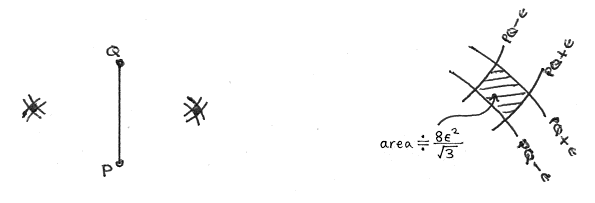
Fix a line PQ by choosing two ley points P and Q.

An equilateral triangle is formed if a third point R falls in either shaded region. If PR and QR are to be within ±ε of the length of PQ, then the probability that a point R will so fall is approximately 2×8ε²/A√3, where A is the area of the map.

With PQ fixed, the mean number of equilateral triangles which will result is approximately 16ε²(n–2)/A√3, and summing over all possible PQ we can expect:

N(Eq.)=	1	×ⁿC₂×	16ε²(n−2)
	3		A√3

the prefixed factor of 1/3 being because in summing over the whole map each equilateral triangle is counted 3 times. Thus:

N(Eq.)=	8n(n−1)(n−2)ε²	.
	3√3A

2014: For an alternative theoretical discussion, see the update to this appendix