Unit 6: The fold Functions
The higher-order function foldr
Many recursively-defined functions on lists in Haskell show a
common pattern of definition.
For example, consider the usual definitions of the functions
sum (which adds together the numerical elements of a list) and
product (which multiples together the numerical elements of a list).
These are shown at the top of Figure 1.
The similarity between these two functions is made even more apparent
if we evaluate them using source reduction.
Doing this on the argument [3, 7, 2]
is shown below the function definitions in Figure 1.
This common pattern of definition is captured by means of the higher-order
function foldr of type
(a -> b -> b) -> b -> [a] -> b.

sum
and product
using foldr.
Another way of bringing out what foldr does is to represent
its final list argument as a binary tree as shown on the left of Figure 2.
Here the expression
foldr (#) u [x1, x2, x3]
is being evaluated.
By looking at this it is clear that the cons nodes have been replaced by the
binary infix operator # and the empty list by the value u.
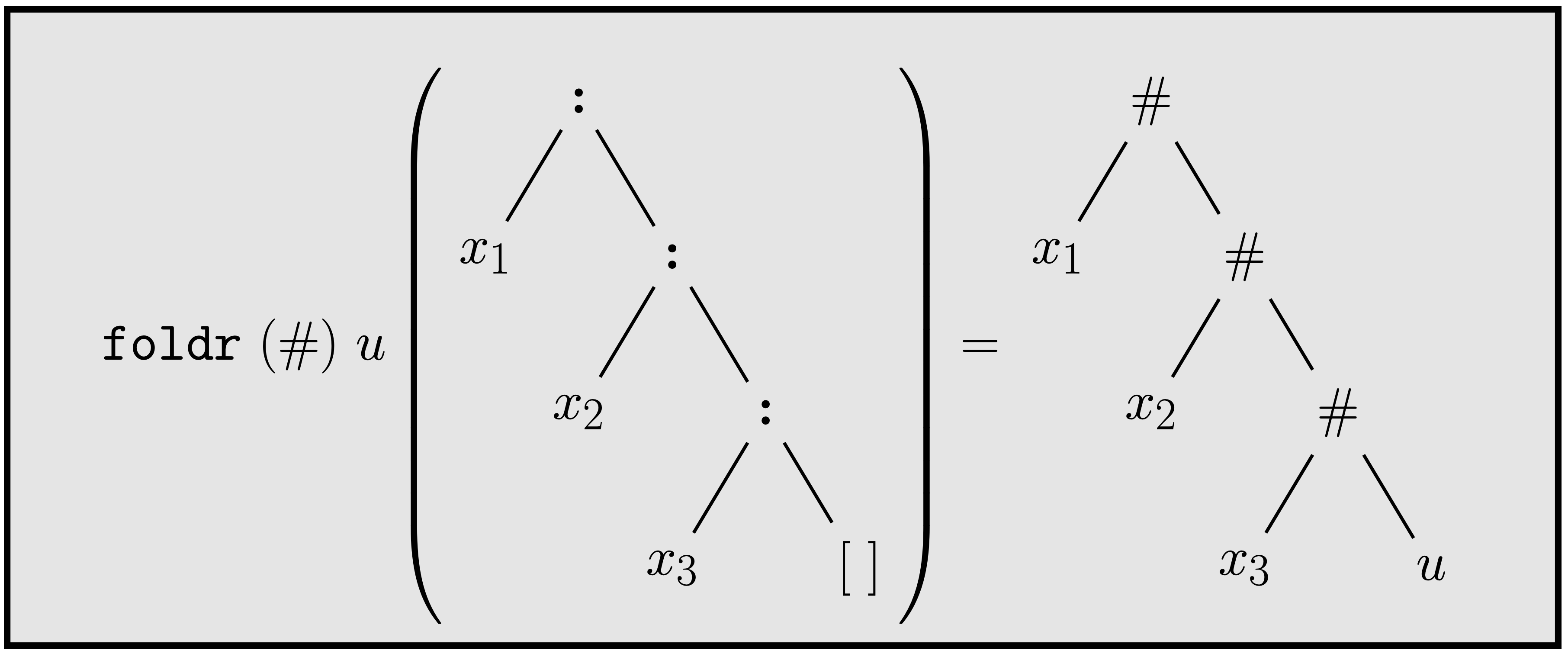
foldr does.
The graphical depiction of what foldr does
shown in Figure 2 should also make it clear that foldr (:) []
is equivalent to the identity function id.
The standard definition of the higher-order function foldr is as follows:
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr op u [] = u
foldr op u (x:xs) = op x (foldr op u xs)
Intuitively, what foldr does can be shown like this,
where # is a binary infix operator:
foldr (#) u [x1, x2, ..., xn] = x1 # (x2 # (...(xn # u)...))
A lot of functions can be defined using foldr,
though other definitions are sometimes preferred for reasons of efficiency.
Here are the definitions of some common functions using foldr:
and, or :: [Bool] -> Bool
and = foldr (&&) True
or = foldr (||) False
sum, product :: Num a => [a] -> a
sum = foldr (+) 0
product = foldr (*) 1
concat :: [[a]] -> [a]
concat = foldr (++) []
length :: [a] -> Int
length = foldr oneplus 0
where oneplus i j = 1 + j
reverse :: [a] -> [a]
reverse = foldr snoc []
where snoc x xs = xs ++ [x]
Defining map and filter with foldr
It is even possible to define the higher-order functions
map and filter by means of foldr:
map f = foldr ((:) . f) []
filter pred = foldr ((++) . sel) []
where sel x
| pred x = [x]
| otherwise = []
fold-map fusion
In the course of writing a Haskell program you might find that you define
a function which applies foldr to the result of applying
map to some argument.
fold-map fusion lets you replace such a definition
by one that only involves foldr:
foldr op u . map f = foldr (op . f) u
The higher-order scanr function
A segment of a list is a list consisting of zero or more adjacent
elements of the original list whose order is preserved.
Thus, the segments of [1, 2, 3] are
[],
[1],
[2],
[3],
[1, 2],
[2, 3]
and [1, 2, 3].
Note that [1, 3] is not a segment of [1, 2, 3].
The tail segments of a list consist of the empty list and
all the segments of the original list which contain its final element.
Thus, the tail segments of [1, 2, 3] are
[],
[3],
[2, 3]
and [1, 2, 3].
It is straightforward to define a Haskell function tails
which returns all the tail segments of a list.
Note that tails produces the list of tail segments in decreasing
order of length, starting with the list xs itself:
tails :: [a] -> [[a]]
tails [] = [[]]
tails xs = [xs] ++ tails (tail xs)
The function scanr applies foldr to every tail segment
of a list, beginning with the longest:
scanr (#) u [x1, x2, x3]
= map (foldr (#) u) (tails [x1, x2, x3])
= [foldr (#) u [x1, x2, x3],
foldr (#) u [x2, x3],
foldr (#) u [x3],
foldr (#) u []]
= [x1 # (x2 # (x3 # u)), x2 # (x3 # u), x3 # u, u]
Folding non-empty lists with foldr1
The function foldr1 can be defined like this:
foldr1 :: (a -> a -> a) -> [a] -> a
foldr1 op [x] = x
foldr1 op (x:xs) = op x (foldr1 op xs)
Intuitively, what foldr1 does can be shown like this,
where # is a binary infix operator:
foldr1 (#) [x1, x2, ..., xn] = x1 # (x2 # (...(xn-1 # xn)...))
Using foldr1 it is easy to define a function that finds the maximum
element of a list:
maxlist = foldr1 max
Here, max is a predefined Haskell function which returns
the larger of its two arguments:
max :: Ord a => a -> a -> a
max x y
| x < y = y
| otherwise = x
The higher-order function foldl
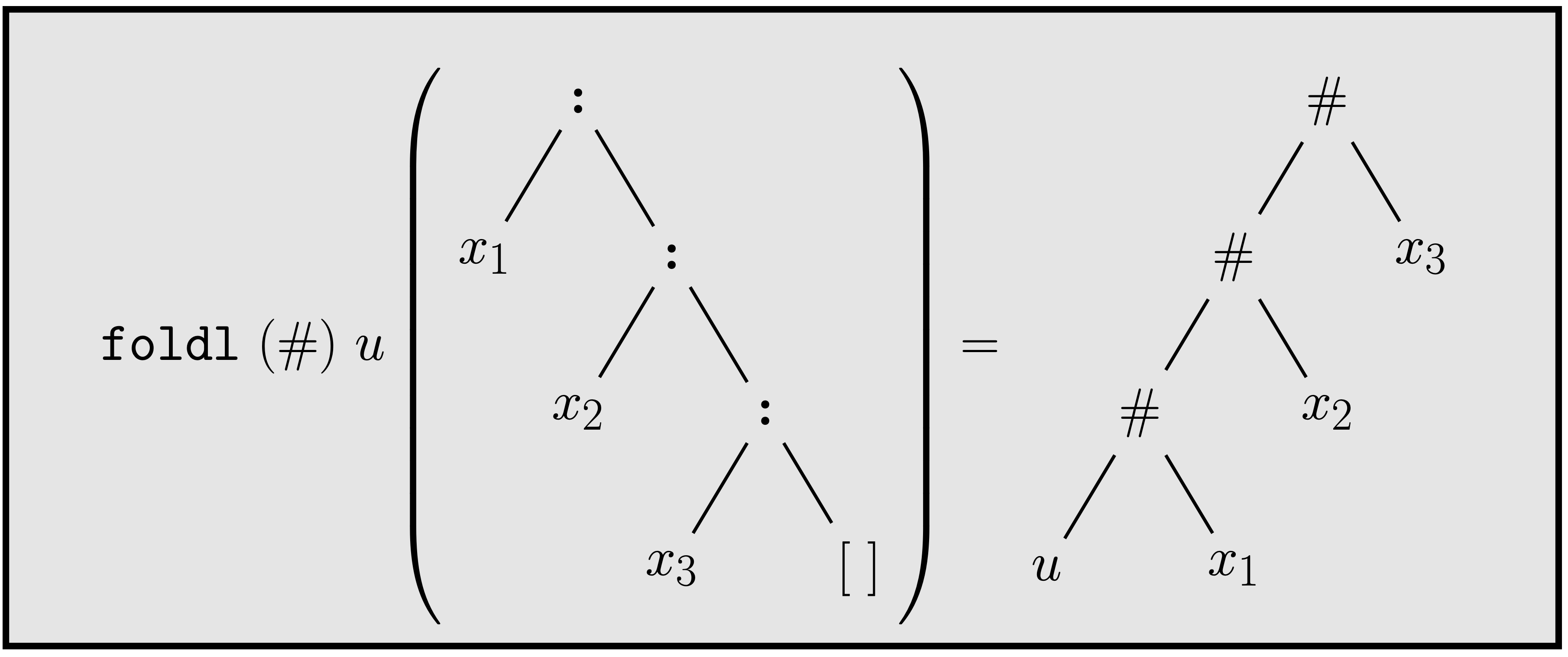
foldl behaves.
The higher-order function foldl can be defined like this:
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl op u [] = u
foldl op u (x:xs) = foldl op (op u x) xs
Intuitively, what foldl does can be shown like this,
where # is a binary infix operator:
foldl (#) u [x1, x2, ..., xn] = (...((u # x1) # x2) # ...) # xn
Many functions can be defined by means of foldl,
though other definitions are sometimes preferred for reasons of efficiency.
Here are the definitions of several common functions using foldl:
and, or :: [Bool] -> Bool
and = foldl (&&) True
or = foldl (||) False
sum, product :: Num a => [a] -> a
sum = foldl (+) 0
product = foldl (*) 1
concat :: [[a]] -> [a]
concat = foldl (++) []
length :: [a] -> Int
length = foldl plusone 0
where plusone i j = i + 1
reverse :: [a] -> [a]
reverse = foldl (flip (:)) []
Here flip is a predefined Haskell function:
flip op x y = op y x.
The definition of reverse in terms of foldl
is more efficient than the obvious definition:
reverse :: [a] -> [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
Duality theorems
The first duality theorem states that,
if # is associative and
u is a unit for #, then
foldr (#) u xs = foldl (#) u xs
Recall that a binary infix operator # is associative if and only if
x # (y # z) = (x # y) # z
and an element u is a unit for
a binary infix operator # if and only if
x # u = u and u # x = u.
The second duality theorem states that
foldr (#) u xs = foldl (◊) u xs
if x # (y ◊ z) = (x # y) ◊ z and
x # u = u ◊ x.
Note that the first duality theorem is a special case of the second.
The third duality theorem simply states:
foldr op u xs = foldl (flip op) u (reverse xs)
The higher-order scanl function
The initial segments of a list are all the segments of that list containing
its first element together with the empty list.
Thus, the initial segments of [1, 2, 3] are
[],
[1],
[1, 2] and [1, 2, 3].
It is straightforward to define a Haskell function inits
which returns all the initial segments of a list.
Note that inits returns the list of initial segments of
xs in increasing order of length, starting with the empty list:
inits :: [a] -> [[a]]
inits [] = [[]]
inits xs = inits (init xs) ++ [xs]
Here, init is a predefined Haskell function which removes the last element
from a non-empty list:
init [1, 2, 3, 4] = [1, 2, 3]
The function scanl applies foldl to every initial segment
of a list, starting with the empty list:
scanl (#) u [x1, x2, x3]
= map (foldl (#) u) (inits [x1, x2, x3])
= [foldl (#) u [],
foldl (#) u [x1],
foldl (#) u [x1, x2],
foldl (#) u [x1, x2, x3]]
= [u, u # x1, (u # x1) # x2, ((u # x1) # x2) # x3]
The infinite list of factorials can then be defined straightforwardly as
scanl (*) 1 [2 .. ].
Folding non-empty lists with foldl1
The function foldl1 can be defined in terms of foldl like this:
foldl1 :: (a -> a -> a) -> [a] -> a
foldl1 op (x:xs) = foldl op x xs
Intuitively, what foldl1 does can be shown like this,
where # is a binary infix operator:
foldl1 (#) [x1, x2, ..., xn] = (...((x1 # x2) # x3)... # xn-1) # xn
Further reading
More information can be found in sections 4.5 and 4.6 of Richard Bird's book Introduction to Functional Programming using Haskell (1998).
© Antoni Diller (21 September 2021)